


Siguiente: Geodésicas
Arriba: Geometría Diferencial y Relatividad
Anterior: Derivadas covariantes
Sea 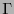 una curva en una
una curva en una  -variedad
-variedad 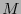 y sea
y sea
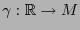 una parametrización de
una parametrización de 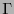 . Sea
. Sea
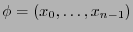 un sistema de coordenadas en un mapa en
un sistema de coordenadas en un mapa en 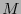 que contenga a la curva
que contenga a la curva 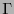 . Entonces
. Entonces
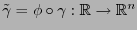 es una curva en
es una curva en 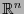 .
Sea
.
Sea
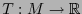 una función diferenciable. Esta función puede identificarse con
una función diferenciable. Esta función puede identificarse con
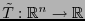 , tal que
, tal que
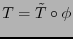 .
.
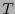 es de transporte paralelo a
es de transporte paralelo a 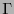 si sus curvas de nivel son paralelas a
si sus curvas de nivel son paralelas a 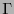 . Es decir, si ocurre que
. Es decir, si ocurre que
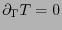 . Así pues, se ha de tener
. Así pues, se ha de tener
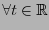 :
:
donde
 .
La derivada covariante se define como el operador:
.
La derivada covariante se define como el operador:
En particular si
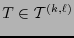 es un
es un  -tensor,
-tensor, 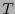 es de transporte paralelo si
es de transporte paralelo si
![\begin{displaymath}
\forall{\bf j}\in[\![0,n-1]\!]^{k},{\bf i}\in[\![0,n-1]\!]^{...
...mma_{i_{\ell}})\,\nabla_{i_{\ell}}T\right)_{{\bf j};{\bf i}}.
\end{displaymath}](img486.png) |
(8.1) |
Si
 es un vector, la ecuación de transporte paralelo (8.1) queda, atendiendo (7.5):
es un vector, la ecuación de transporte paralelo (8.1) queda, atendiendo (7.5):
y por tanto
![\begin{displaymath}
\forall j\in[\![0,n-1]\!]:\ D_{\Gamma}(u_j)\, + \sum_{k=0}^{n-1} u_k \sum_{i=0}^{n-1}c_{k,ij}D_{\Gamma}(\gamma_i) = 0.
\end{displaymath}](img488.png) |
(8.2) |
Ahora, supongamos que la curva 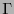 sea compatible con el tensor de métrica
sea compatible con el tensor de métrica
![$G=\left(g_{ij}\right)_{i,j\in[\![0,n-1]\!]}$](img489.png) , es decir
, es decir
Entonces, si
 y
y
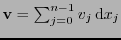 son dos vectores de transporte paralelo según
son dos vectores de transporte paralelo según 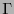 , se tiene
, se tiene
o sea, el producto escalar
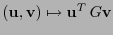 (y cualquier otra noción geométrica asociada a él) es de transporte paralelo a
(y cualquier otra noción geométrica asociada a él) es de transporte paralelo a 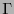 .
.
Supongamos ahora que
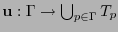 es un campo de vectores que satisfagan la ecuación de transporte paralelo (8.2). Supongamos asímismo que fijo
es un campo de vectores que satisfagan la ecuación de transporte paralelo (8.2). Supongamos asímismo que fijo
 existe un campo de matrices
existe un campo de matrices
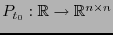 tal que
tal que
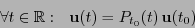 |
(8.3) |
por lo que el campo 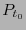 se llama propagador de paralelismo. Observando (8.2) definamos
se llama propagador de paralelismo. Observando (8.2) definamos
Entonces (8.2) se replantea como
 O sea
O sea
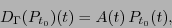 |
(8.4) |
la cual se conoce como ecuación de Dyson y es similar a la de onda de Schrödinger. Equivalentemente
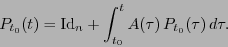 |
(8.5) |
La ecuación integral (8.5) tiene solución de la forma
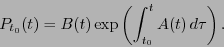 |
(8.6) |
Así pues, (8.3) y (8.6) dan un vector de transporte paralelo a 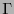 .
.



Siguiente: Geodésicas
Arriba: Geometría Diferencial y Relatividad
Anterior: Derivadas covariantes
Guillermo M. Luna
2011-01-03
![]() una curva en una
una curva en una ![]() -variedad
-variedad ![]() y sea
y sea
![]() una parametrización de
una parametrización de ![]() . Sea
. Sea
![]() un sistema de coordenadas en un mapa en
un sistema de coordenadas en un mapa en ![]() que contenga a la curva
que contenga a la curva ![]() . Entonces
. Entonces
![]() es una curva en
es una curva en ![]() .
Sea
.
Sea
![]() una función diferenciable. Esta función puede identificarse con
una función diferenciable. Esta función puede identificarse con
![]() , tal que
, tal que
![]() .
.
![]() es de transporte paralelo a
es de transporte paralelo a ![]() si sus curvas de nivel son paralelas a
si sus curvas de nivel son paralelas a ![]() . Es decir, si ocurre que
. Es decir, si ocurre que
![]() . Así pues, se ha de tener
. Así pues, se ha de tener
![]() :
:
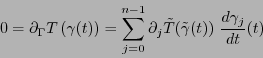
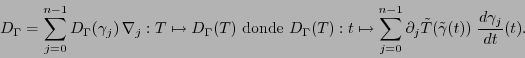
![\begin{eqnarray*}
0 &=& \sum_{i=0}^{n-1}D_{\Gamma}(\gamma_i)\,\nabla_{i}(u) \\
...
...0}^{n-1} u_k c_{k,ij}D_{\Gamma}(\gamma_i)\,\right]\,\mbox{d}x_j
\end{eqnarray*}](img487.png)
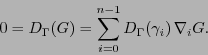
![]() es un campo de vectores que satisfagan la ecuación de transporte paralelo (8.2). Supongamos asímismo que fijo
es un campo de vectores que satisfagan la ecuación de transporte paralelo (8.2). Supongamos asímismo que fijo
![]() existe un campo de matrices
existe un campo de matrices
![]() tal que
tal que
![\begin{displaymath}\forall j,k\in[\![0,n-1]\!]:\ a_{jk}(t) = - \sum_{i=0}^{n-1}c_{k,ij}D_{\Gamma}(\gamma_i)({\bf u}(t)).\end{displaymath}](img498.png)