


Siguiente: Transporte paralelo
Arriba: Geometría Diferencial y Relatividad
Anterior: Variedades diferenciables
Sea
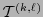 la colección de
la colección de  -tensores. La derivada covariante es una aplicación
-tensores. La derivada covariante es una aplicación
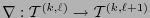 de manera que
de manera que
- sea aditiva
-
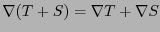 , y
, y
- cumpla la regla de Leibniz
-
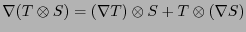 .
.
Por ejemplo, para
 , los
, los 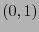 -tensores son funcionales. Si
-tensores son funcionales. Si
 entonces:
entonces:
 |
(7.1) |
Para cada
![$i\in[\![0,n-1]\!]$](img449.png) ,
,
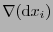 es un ``bifuncional''. Expresémoslo como
es un ``bifuncional''. Expresémoslo como
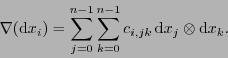 |
(7.2) |
De hecho, de (7.2), para dos índices
![$j',k'\in[\![0,n-1]\!]$](img452.png) :
:
Así pues,
![\begin{displaymath}
\forall i,j,k\in[\![0,n-1]\!]:\ \ c_{i,jk} = \nabla(\mbox{d}{x_i})(x_{j},x_{k}),
\end{displaymath}](img454.png) |
(7.3) |
y éstos se llaman coeficientes de conexión o de Christoffel. (En muchos textos se les suele denotar como
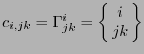 .) Al
.) Al  -tensor cuyas componentes son los coeficientes de Christoffel se le llama de conexión.
Al sustituir (7.2) en (7.1), se obtiene
-tensor cuyas componentes son los coeficientes de Christoffel se le llama de conexión.
Al sustituir (7.2) en (7.1), se obtiene
(en la tercera igualdad hemos hecho varios renombramientos de índices).
Por tanto, el 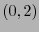 -tensor
-tensor
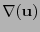 tiene como arreglo de componentes a
tiene como arreglo de componentes a
![\begin{displaymath}
C_{(0,1)} = \left[u_j + \sum_{k=0}^{n-1} u_k c_{k,ij}\right]_{0\leq i,j\leq n-1}.
\end{displaymath}](img459.png) |
(7.4) |
Para cada
![$i\in[\![0,n-1]\!]$](img449.png) definamos el
definamos el 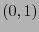 -tensor
-tensor
![\begin{displaymath}
\nabla_i({\bf u}) = \sum_{j=0}^{n-1} \left[\partial_{x_i}u_j + \sum_{k=0}^{n-1} u_k c_{k,ij}\right]\,\mbox{d}x_j.
\end{displaymath}](img460.png) |
(7.5) |
De manera un poco más general, para  e
e
![${\bf i}\in[\![0,n-1]\!]^{\ell}$](img462.png) sea
sea
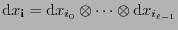 . Si se expresa
. Si se expresa
![\begin{displaymath}
\nabla(\mbox{d}{x_{\bf i}}) = \sum_{{\bf j}\in[\![0,n-1]\!]^...
...f j},j_{\ell}}\,\mbox{d}x_{\bf j}\otimes\mbox{d}x_{j_{\ell}},
\end{displaymath}](img464.png) |
(7.6) |
entonces para cualquier
 donde
donde
![$T = \sum_{{\bf j}\in[\![0,n-1]\!]^{\ell}} u_{\bf j}\,\mbox{d}x_{\bf j}$](img466.png) , el arreglo de componentes de
, el arreglo de componentes de 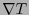 es
es
![\begin{displaymath}
C_{(0,\ell)} = \left[u_{\bf j} + \sum_{{\bf k}\in[\![0,n-1]\...
...{\bf j},j_{\ell})\in[\![0,n-1]\!]^{\ell}\times[\![0,n-1]\!]}.
\end{displaymath}](img468.png) |
(7.7) |
Para cada
![${\bf i}\in[\![0,n-1]\!]^{\ell}$](img462.png) definamos el
definamos el 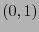 -tensor
-tensor
![\begin{displaymath}
\nabla_{\bf i}({\bf u}) = \sum_{j=0}^{n-1} \left[\partial_{{...
...]^{\ell}} u_{\bf k} c_{{\bf k},{\bf i}j}\right]\,\mbox{d}x_j.
\end{displaymath}](img469.png) |
(7.8) |
Supongamos ahora que
![$J_p=\left[\partial_{y_i}x_j(p)\right]_{0\leq i,j\leq n-1}$](img392.png) es la matriz jacobiana de un cambio de coordenadas a
es la matriz jacobiana de un cambio de coordenadas a
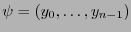 . Consideremos, para aligerar la notación,
. Consideremos, para aligerar la notación,  . De manera similar a (6.4),
. De manera similar a (6.4),
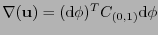 , y como en (6.5),
, y como en (6.5),
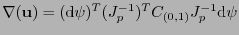 . Por tanto, necesariamente
. Por tanto, necesariamente
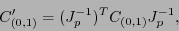 |
(7.9) |
donde  es el arreglo de componentes de
es el arreglo de componentes de
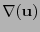 respecto al sistema de coordenadas
respecto al sistema de coordenadas  , lo cual concuerda también con la relación de cambio de variables (3.3). De manera equivalente, (7.9) se escribe,
, lo cual concuerda también con la relación de cambio de variables (3.3). De manera equivalente, (7.9) se escribe,



Siguiente: Transporte paralelo
Arriba: Geometría Diferencial y Relatividad
Anterior: Variedades diferenciables
Guillermo M. Luna
2011-01-03
![]() la colección de
la colección de ![]() -tensores. La derivada covariante es una aplicación
-tensores. La derivada covariante es una aplicación
![]() de manera que
de manera que

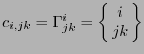 .) Al
.) Al ![\begin{eqnarray*}
\nabla({\bf u})
&=& \sum_{i=0}^{n-1} \left(\nabla u_i\right)\...
..._{k=0}^{n-1} u_k c_{k,ij}\right]\,\mbox{d}x_i\otimes\mbox{d}x_j
\end{eqnarray*}](img457.png)
![\begin{displaymath}\forall i',j'\in[\![0,n-1]\!]:\ \ u'_{j'} + \sum_{k'=0}^{n-1}...
..._j + \sum_{k=0}^{n-1} u_k c_{k,ij}\right)\partial_{x_j}(y_{j'})\end{displaymath}](img476.png)