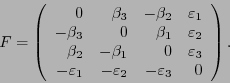


Siguiente: Contracción .
Arriba: Geometría Diferencial y Relatividad
Anterior: Marcos de referencia
Tensores
Sean
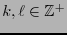 dos enteros positivos. Una
dos enteros positivos. Una  -forma multilineal es una transformación
-forma multilineal es una transformación
tal que para cada
![$i\in[\![0,k+\ell-1]\!]$](img121.png) , fijos los
, fijos los 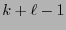 argumentos
argumentos
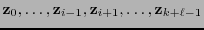 , la aplicación seccional
, la aplicación seccional
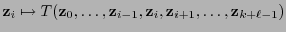 es lineal.
es lineal.
Una  -forma multilineal se dice ser también un
-forma multilineal se dice ser también un  -tensor y la pareja
-tensor y la pareja  el orden del tensor.
el orden del tensor.
De manera natural, un escalar se identifica con un 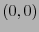 -tensor,
-tensor,
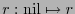 , un vector en
, un vector en  con un
con un  -tensor,
-tensor,
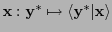 , y una funcional lineal con un
, y una funcional lineal con un 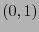 -tensor,
-tensor,
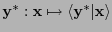 .
.
Sea
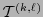 la colección de
la colección de  -tensores. Evidentemente,
-tensores. Evidentemente,
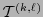 es un espacio vectorial real.
es un espacio vectorial real.
Para dos tensores cualesquiera 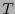 ,
,  , de órdenes respectivos
, de órdenes respectivos  ,
, 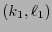 , su producto tensorial
, su producto tensorial 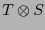 es el
es el
 -tensor
-tensor
Se ve entonces que una base de
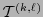 está constituída por los
está constituída por los  -tensores
-tensores
con
![$({\bf j};{\bf i})\in[\![0,3]\!]^k\times[\![0,3]\!]^{\ell}$](img140.png) ,
por lo que la dimensión de
,
por lo que la dimensión de
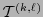 es
es 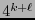 . De hecho para todo
. De hecho para todo
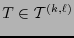 :
:
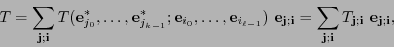 |
(3.1) |
y de esta expresión puede verse que vale también
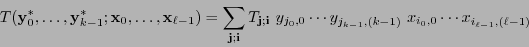 |
(3.2) |
Los coeficientes
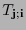 son las componentes de la
son las componentes de la  -forma multilineal
-forma multilineal 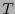 respecto a la base
respecto a la base
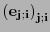 . De manera puramente ideal, el
. De manera puramente ideal, el  -tensor
-tensor 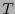 puede ser visto como la matriz, de dimensión
puede ser visto como la matriz, de dimensión  ,
,
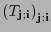 .
.
Si 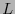 es una transformación de Lorentz y
es una transformación de Lorentz y 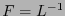 es la nueva base determinada por el cambio
es la nueva base determinada por el cambio 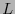 , entonces las componentes de
, entonces las componentes de 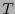 respecto a la base
respecto a la base 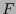 son
son
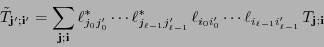 |
(3.3) |
donde
![$L=\left[\ell_{ij}\right]_{i,j\in[\![0,3]\!]}$](img150.png) y
y
![$(L^{-1})^T=\left[\ell^*_{ij}\right]_{i,j\in[\![0,3]\!]}$](img151.png) .
.
Evidentemente, si
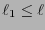 y
y
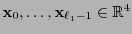 están fijos entonces la forma seccional
están fijos entonces la forma seccional
es un
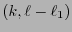 -tensor. Similarmente, si
-tensor. Similarmente, si 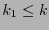 e
e
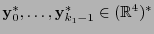 están fijos entonces la forma seccional
están fijos entonces la forma seccional
es un 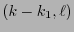 -tensor.
-tensor.
Como ejemplos de tensores están los siguientes:
- Productos escalares
- Todo
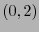 -tensor se dice ser un producto escalar y, respecto a una base fija, queda determinado por una matriz
-tensor se dice ser un producto escalar y, respecto a una base fija, queda determinado por una matriz
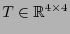 .
.
- Norma de Minkowski
- Naturalmente, la matriz
![$M=\mbox{diag}[1\ \ 1\ \ 1\ \ -1]$](img162.png) definida por (1.1) es un producto escalar.
definida por (1.1) es un producto escalar.
- Inversa de Minkowski
- La matriz
 , que de hecho coincide con
, que de hecho coincide con 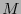 , determina un
, determina un 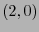 -tensor, llamado inverso de
-tensor, llamado inverso de 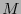 .
.
- Producto interno
- Un
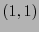 -tensor queda determinado por la matriz identidad
-tensor queda determinado por la matriz identidad
![$\mbox{Id}_4=\mbox{diag}[1\ \ 1\ \ 1\ \ 1]$](img167.png) :
:
 , es el producto interno usual, con el Teorema de Representación de Riesz de por medio.
, es el producto interno usual, con el Teorema de Representación de Riesz de por medio.
- Tensor de Levi-Civitá
- Sea
![$\mbox{LC}=\left[\varepsilon_{ijk\ell}\right]_{i,j,k,\ell\in[\![0,3]\!]}\in\mathbb{R}^{4\times 4\times 4\times 4}$](img169.png) , donde
, donde
 si algunos dos de los índices
si algunos dos de los índices 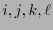 coinciden o bien es el signo de la permutación
coinciden o bien es el signo de la permutación 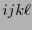 en otro caso. Entonces
en otro caso. Entonces 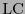 determina un
determina un 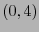 -tensor, llamado de Levi-Civitá.
-tensor, llamado de Levi-Civitá.
De manera más general para una lista de 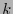 -índices
-índices
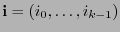 sea
sea
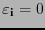 si
si  no es una permutación y sea
no es una permutación y sea
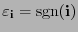 en otro caso; y para una pareja de listas de índices
en otro caso; y para una pareja de listas de índices
![$({\bf j};{\bf i})\in[\![0,3]\!]^{k+\ell}$](img180.png) sea
sea
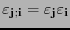 . Entonces
. Entonces
![$\mbox{LC}_{k\ell}=\left[\varepsilon_{{\bf j};{\bf i}}\right]_{({\bf j};{\bf i})\in[\![0,3]\!]^{k+\ell}}$](img182.png) determina un
determina un  -tensor, llamado también de Levi-Civitá.
-tensor, llamado también de Levi-Civitá.
- Intensidad de campo electromagnético
- Para 6 valores reales
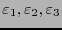 ,
,
 sea
sea
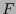 es una matriz antisimétrica y define un
es una matriz antisimétrica y define un  -tensor.
-tensor.
Un operador que actúa sobre tensores es el siguiente.
Subsections



Siguiente: Contracción .
Arriba: Geometría Diferencial y Relatividad
Anterior: Marcos de referencia
Guillermo M. Luna
2011-01-03
![]() dos enteros positivos. Una
dos enteros positivos. Una ![]() -forma multilineal es una transformación
-forma multilineal es una transformación
![]() -forma multilineal se dice ser también un
-forma multilineal se dice ser también un ![]() -tensor y la pareja
-tensor y la pareja ![]() el orden del tensor.
el orden del tensor.
![]() -tensor,
-tensor,
![]() , un vector en
, un vector en ![]() con un
con un ![]() -tensor,
-tensor,
![]() , y una funcional lineal con un
, y una funcional lineal con un ![]() -tensor,
-tensor,
![]() .
.
![]() la colección de
la colección de ![]() -tensores. Evidentemente,
-tensores. Evidentemente,
![]() es un espacio vectorial real.
es un espacio vectorial real.
![]() ,
, ![]() , de órdenes respectivos
, de órdenes respectivos ![]() ,
, ![]() , su producto tensorial
, su producto tensorial ![]() es el
es el
![]() -tensor
-tensor
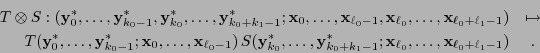
![]() es una transformación de Lorentz y
es una transformación de Lorentz y ![]() es la nueva base determinada por el cambio
es la nueva base determinada por el cambio ![]() , entonces las componentes de
, entonces las componentes de ![]() respecto a la base
respecto a la base ![]() son
son
![]() y
y
![]() están fijos entonces la forma seccional
están fijos entonces la forma seccional
![]() -índices
-índices
![]() sea
sea
![]() si
si ![]() no es una permutación y sea
no es una permutación y sea
![]() en otro caso; y para una pareja de listas de índices
en otro caso; y para una pareja de listas de índices
![]() sea
sea
![]() . Entonces
. Entonces
![]() determina un
determina un ![]() -tensor, llamado también de Levi-Civitá.
-tensor, llamado también de Levi-Civitá.