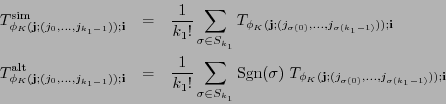Sea
![]() un
un ![]() -tensor y sean
-tensor y sean ![]() dos índices distintos en el intervalo
dos índices distintos en el intervalo ![]() . Para
. Para
![]() y
y
![]() sea
sea
![]() el arreglo que se obtiene de insertar
el arreglo que se obtiene de insertar ![]() y
y ![]() en las posiciones
en las posiciones ![]() y
y ![]() , respectivamente, dentro de
, respectivamente, dentro de ![]() .
.
![]() es simétrico respecto a
es simétrico respecto a ![]() si las entradas de
si las entradas de ![]() no cambian al intercambiar los índices en las posiciones
no cambian al intercambiar los índices en las posiciones ![]() y
y ![]() :
:
![]() es antisimétrico, o alternante, respecto a
es antisimétrico, o alternante, respecto a ![]() si las entradas de
si las entradas de ![]() cambian de signo al intercambiar los índices en las posiciones
cambian de signo al intercambiar los índices en las posiciones ![]() y
y ![]() :
:
![]() y su inversa, al estar dados por matrices diagonales, son simétricos. Los tensores de Levi-Civitá y de intensidad de campo electromagnético son alternantes. El producto interno, al ser un
y su inversa, al estar dados por matrices diagonales, son simétricos. Los tensores de Levi-Civitá y de intensidad de campo electromagnético son alternantes. El producto interno, al ser un ![]() -tensor, es simétrico y alternante a la vez, por mera vacuidad.
-tensor, es simétrico y alternante a la vez, por mera vacuidad.
Para un conjunto ![]() de
de ![]() índices en
índices en ![]() , una
, una ![]() -ada
-ada
![]() y una
y una ![]() -ada
-ada
![]() sea
sea
![]() la
la ![]() -ada obtenida al colocar (intercalar) cada índice
-ada obtenida al colocar (intercalar) cada índice ![]() en la posición
en la posición ![]() dentro de
dentro de ![]() .
.
Sea
![]() un
un ![]() -tensor arbitrario. La simetrización y la antisimetrización de
-tensor arbitrario. La simetrización y la antisimetrización de ![]() se definen haciendo para cada
se definen haciendo para cada
![]() ,
,
![]() e
e
![]() :
: