


Siguiente: Longitudes
Arriba: Formas diferenciales
Anterior: Formas diferenciales
Sean
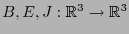 campos vectoriales magnético, eléctrico, y de corriente, respectivamente y sea
campos vectoriales magnético, eléctrico, y de corriente, respectivamente y sea
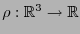 el campo escalar de densidad de carga. Las ecuaciones de Maxwell son
el campo escalar de densidad de carga. Las ecuaciones de Maxwell son
 |
(4.3) |
donde
![$\nabla = [\partial_x\ \ \partial_y\ \ \partial_z]^T$](img277.png) . Así,
. Así, 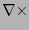 ,
, 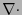 son los operadores rotacional y divergencia respectivamente. Como acordamos desde un principio usemos
son los operadores rotacional y divergencia respectivamente. Como acordamos desde un principio usemos
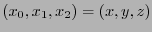 para nombrar a las coordenadas espaciales y
para nombrar a las coordenadas espaciales y 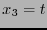 a la temporal.
a la temporal.
Al hacer
![$F_i =\left[\varepsilon_{ijk}\right]_{j,k\in\{0,1,2\}}$](img281.png) se tiene
se tiene
![$\nabla\times B=\left[\nabla^TF_iB\right]_{i\in\{0,1,2\}}$](img282.png) . Ampliemos los vectores como
. Ampliemos los vectores como
-
![$\nabla = [\partial_0\ \ \partial_1\ \ \partial_2\ \ \partial_3]^T$](img283.png) ,
,
-
![$B=[b_0\ \ b_1\ \ b_2\ \ 0]^T$](img284.png) ,
,
-
![$F =\left[\alpha_{ijk\ell}\right]_{i,j,k,\ell\in\{0,1,2,3\}}$](img285.png) , donde
, donde
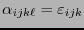 si
si
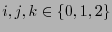 y
y
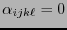 en otro caso, por tanto
en otro caso, por tanto
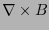 se expresa como un tensor
se expresa como un tensor
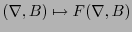 ,
,
-
![$E=[e_0\ \ e_1\ \ e_2\ \ 0]^T$](img291.png) ,
,
- se tiene
![$\nabla^T[0\ \ 0\ \ 0\ \ 1] = \partial_t$](img292.png) y
y
![$\nabla^T[1\ \ 1\ \ 1\ \ 0] = \partial_x+\partial_y+\partial_z$](img293.png) es el operador divergencia
es el operador divergencia 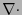 ,
,
-
![$J=[j_0\ \ j_1\ \ j_2\ \ \rho]^T$](img294.png) ,
,
y en consecuencia las dos ecuaciones a la izquierda de (4.3) se plantean como un sistema de la forma
![\begin{displaymath}
\forall i\in[\![0,3]\!]:\ G^{\mbox{\scriptsize izq}}_i(\nabla;B,E)=4\pi J_i
\end{displaymath}](img295.png) |
(4.4) |
Similarmente las dos ecuaciones a la derecha de (4.3) como un sistema
![\begin{displaymath}
\forall i\in[\![0,3]\!]:\ G^{\mbox{\scriptsize der}}_i(\nabla;B,E)=0.
\end{displaymath}](img296.png) |
(4.5) |
Ahora bien, el sistema (4.5) puede plantearse como una ecuación de la forma d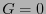 para un cierto tensor
para un cierto tensor 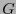 que, en consecuencia, ha de ser cerrado. En el espacio de Minkowski, todo tensor cerrado es exacto, por tanto, ha de existir un tensor
que, en consecuencia, ha de ser cerrado. En el espacio de Minkowski, todo tensor cerrado es exacto, por tanto, ha de existir un tensor 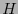 tal que
tal que 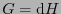 . El tensor
. El tensor 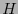 se llama potencia vectorial, en particular, su componente temporal es la potencia escalar.
se llama potencia vectorial, en particular, su componente temporal es la potencia escalar.
Las ecuaciones (4.4) pueden ser planteadas de la forma
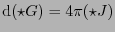 .
.
Debido a (4.2), se tiene que las ecuaciones tensoriales son invariantes bajo las transformaciones
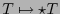 y
y
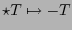 .
.



Siguiente: Longitudes
Arriba: Formas diferenciales
Anterior: Formas diferenciales
Guillermo M. Luna
2011-01-03
![]() se tiene
se tiene
![]() . Ampliemos los vectores como
. Ampliemos los vectores como
![]() para un cierto tensor
para un cierto tensor ![]() que, en consecuencia, ha de ser cerrado. En el espacio de Minkowski, todo tensor cerrado es exacto, por tanto, ha de existir un tensor
que, en consecuencia, ha de ser cerrado. En el espacio de Minkowski, todo tensor cerrado es exacto, por tanto, ha de existir un tensor ![]() tal que
tal que ![]() . El tensor
. El tensor ![]() se llama potencia vectorial, en particular, su componente temporal es la potencia escalar.
se llama potencia vectorial, en particular, su componente temporal es la potencia escalar.
![]() .
.
![]() y
y
![]() .
.