Sean ![]() las regiones temporal, lumínica y espacial, respectivamente, definidas por las relaciones (1.3), del espacio-tiempo
las regiones temporal, lumínica y espacial, respectivamente, definidas por las relaciones (1.3), del espacio-tiempo ![]() .
.
Sea
![]() la parametrización de una curva
la parametrización de una curva ![]() de clase
de clase ![]() . Sea
. Sea ![]() la derivada de
la derivada de ![]() , es decir, el vector tangente a la curva
, es decir, el vector tangente a la curva ![]() en cada punto. Se define el elemento de línea:
en cada punto. Se define el elemento de línea:
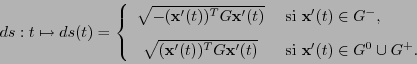
Supongamos en lo sucesivo que ![]() es una curva en la region temporal
es una curva en la region temporal ![]() y que, fijo
y que, fijo
![]() la función
la función
![]() es inyectiva. Sea
es inyectiva. Sea
![]() su función inversa:
su función inversa:
![]() y
y
![]() . Por la Regla de la Cadena:
. Por la Regla de la Cadena:
Si la partícula en movimiento tiene masa ![]() , entonces el vector energía-momento es
, entonces el vector energía-momento es
![]() (omitimos aquí el argumento
(omitimos aquí el argumento ![]() ), donde la energía es propiamente la coordenada temporal, y por tanto
), donde la energía es propiamente la coordenada temporal, y por tanto ![]() , que corresponde a la famosa ecuación de Einstein
, que corresponde a la famosa ecuación de Einstein ![]() , pues hemos considerado
, pues hemos considerado ![]() en este contexto. En una situación en reposo, la velocidad tangencial es
en este contexto. En una situación en reposo, la velocidad tangencial es
![]() . Supongamos que la curva
. Supongamos que la curva ![]() es el eje
es el eje ![]() , parametrizada a una velocidad
, parametrizada a una velocidad ![]() . Aplicando una transformación de Lorentz
. Aplicando una transformación de Lorentz ![]() , que sea una rotación espacio-temporal de la forma (1.5), se ha de tener
, que sea una rotación espacio-temporal de la forma (1.5), se ha de tener
En la mecánica de Newton, se tiene
![]() . El análogo relativista es
. El análogo relativista es
Considerando campos electromagnéticos, la fuerza queda dada por una expresión
![]() , donde
, donde ![]() es la carga de la partícula sujeta a los campos. De manera similar a como se hizo al final de la sección anterior se puede obtener una expresión
es la carga de la partícula sujeta a los campos. De manera similar a como se hizo al final de la sección anterior se puede obtener una expresión
![]() donde cada
donde cada ![]() es un tensor.
es un tensor.