


Posterior: Bibliography
Arriba: Algoritmo cuántico para el
Anterior: Elementos con orden potencia
Dejemos de suponer que el orden 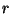 de
de 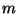 sea una potencia de 2 en
sea una potencia de 2 en 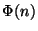 . Siguiendo la misma línea que en el caso anterior, sea
. Siguiendo la misma línea que en el caso anterior, sea 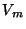 definido como en
la ec. (11). Sea
definido como en
la ec. (11). Sea
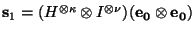 y
y
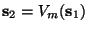 . Reagrupando los términos según se hizo en la ec. (12) se puede escribir
. Reagrupando los términos según se hizo en la ec. (12) se puede escribir
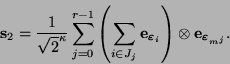 |
(16) |
donde los conjuntos  son clases de equivalencia, congruentes con
son clases de equivalencia, congruentes con 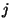 , módulo
, módulo 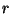 , pero ahora no son de la misma cardinalidad. Si
, pero ahora no son de la misma cardinalidad. Si
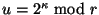 y
y
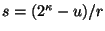 entonces
entonces 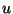 clases tendrán
clases tendrán 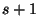 elementos y las restantes tendrán
elementos y las restantes tendrán 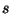 elementos. Definamos
elementos. Definamos  para
para  y
y 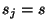 para
para
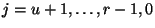 . Entonces el estado que representa el tomar una medición, como en la ec. (13), es, para algún
. Entonces el estado que representa el tomar una medición, como en la ec. (13), es, para algún
![$j_0\in[\![0,r-1]\!]$](img453.png) :
:
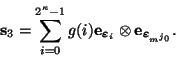 |
(17) |
donde
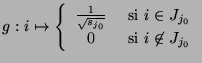
Calculando la transformada inversa discreta de Fourier y reagrupando términos, como en la ec. (14), se obtiene
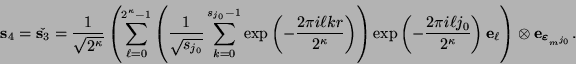 |
(18) |
pero en este caso el coeficiente que involucra a la suma interior nunca se anula (como 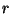 no necesariamente divide a
no necesariamente divide a 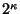 , aquí no se está sumando un ``juego completo'' de raices
, aquí no se está sumando un ``juego completo'' de raices 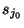 -ésimas de la unidad). Al tomar una medición del primer qubit, la probabilidad de que se elija a
-ésimas de la unidad). Al tomar una medición del primer qubit, la probabilidad de que se elija a
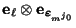 es entonces
es entonces
y los máximos de esos valores corresponden a enteros
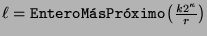 ,
,
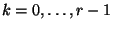 . Supongamos que tras una medición se haya elegido
. Supongamos que tras una medición se haya elegido
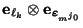 , con
, con
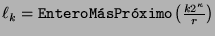 . Entonces, al dividir ese índice entre
. Entonces, al dividir ese índice entre 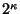 se obtiene
se obtiene
 , y de aquí se quiere conocer
, y de aquí se quiere conocer 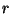 . Para esto hay que recordar la noción de fracciones continuadas.
. Para esto hay que recordar la noción de fracciones continuadas.
Si  es un número racional no-negativo, su fracción continuada es
es un número racional no-negativo, su fracción continuada es
![\begin{displaymath}
\frac{p}{q} = a_0 + \frac{1}{a_1 + \frac{1}{\cdots + \frac{1}{a_v}}} = \left[a_0,a_1,\ldots,a_v\right]
\end{displaymath}](img465.png) |
(19) |
donde
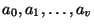 son enteros no-negativos. Para cada
son enteros no-negativos. Para cada 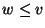 , la fracción continuada
, la fracción continuada
![$\left[a_0,a_1,\ldots,a_w\right]$](img468.png) se dice ser el
se dice ser el 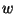 -ésimo convergente de
-ésimo convergente de  , y, en efecto, cada convergente es una aproximación racional a
, y, en efecto, cada convergente es una aproximación racional a  . El algoritmo para calcular fracciones continuadas es directo:
. El algoritmo para calcular fracciones continuadas es directo:
- Entrada.
-
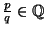 .
.
- Salida.
-
![$\left[a_0,a_1,\ldots,a_v\right]$](img471.png) : fracción continuada que representa a
: fracción continuada que representa a
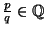 .
.
- Procedimiento
- FracciónContinuada
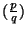
- Sean inicialmente
![$\mbox{\it lst}:=[]$](img473.png) (la lista vacía) y
(la lista vacía) y
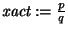 .
.
- Mientras el denominador de
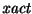 sea mayor que 1 hágase
sea mayor que 1 hágase
- sea
 ;
;
- escríbase
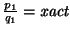 ;
;
- actualícese
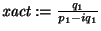 ;
;
- actualícese
![$\mbox{\it lst}:=\mbox{\it lst}*[i]$](img479.png) .
.
- Actualícese
![$\mbox{\it lst}:=\mbox{\it lst}*[\mbox{\it xact}]$](img480.png) .
.
- Dése como resultado
 .
.
Así pues, luego de haber realizado una medición y haber obtenido el valor
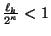 , se calcula su fracción continuada
, se calcula su fracción continuada
![$\left[a_0,a_1,\ldots,a_v\right]$](img471.png) (
(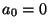 ) y los correspondientes convergentes
) y los correspondientes convergentes
![$\left[c_0,c_1,\ldots,c_v\right]$](img484.png) (también
(también 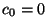 ), y entre éstos se selecciona a aquellos cuyos denominadores
), y entre éstos se selecciona a aquellos cuyos denominadores  sean menores que
sean menores que  , los cuales han de ser divisores del orden
, los cuales han de ser divisores del orden 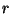 de
de 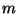 .
.
En resumen, esta vez el algoritmo para localizar divisores de órdenes de elementos es el siguiente:
- Entrada.
-
 ,
, 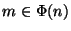 .
.
- Salida.
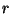 tal que
tal que  .
.
- Procedimiento
- DivisorOrden
- Sea
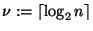 ,
,
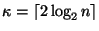 .
.
- Defínase
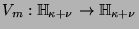 como en la ec. (11).
como en la ec. (11).
- Sea
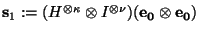 .
.
- Sea
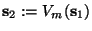 .
.
- Sea
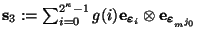 el estado equivalente a ``tomar una medición'' en
el estado equivalente a ``tomar una medición'' en
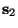 . Entonces
. Entonces 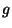 queda determinada como en la ec. (17).
queda determinada como en la ec. (17).
- Sea
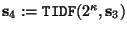 la transformada inversa discreta de Fourier de
la transformada inversa discreta de Fourier de
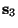 .
.
- Sea
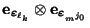 una medición de
una medición de
 .
.
- Si
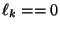 repítase desde el paso 3. En otro caso
repítase desde el paso 3. En otro caso
- sea
![$\left[a_0,a_1,\ldots,a_v\right]:=\mbox{\tt Fracci\'onContinuada}\left(\frac{\ell_k}{2^{\kappa}}\right)$](img489.png) ;
;
- sea
![$\left[c_0,c_1,\ldots,c_v\right]$](img484.png) la lista de convergentes; y
la lista de convergentes; y
- dése como resultado la lista de denominadores, de los convergentes, que sean menores que
 .
.
Habiendo obtenido divisores de órdenes, se puede proceder a obtener los órdenes de manera similar a como se bosquejó en el procedimiento OrdenPotencia2, mas en este caso hay que llevar un recuento de las varias posibilidades de divisores que arroja el procedimiento DivisorOrden descrito arriba.



Posterior: Bibliography
Arriba: Algoritmo cuántico para el
Anterior: Elementos con orden potencia
Guillermo Morales-Luna gmorales at cs.cinvestav.mx
2003-12-11
![]() de
de ![]() sea una potencia de 2 en
sea una potencia de 2 en ![]() . Siguiendo la misma línea que en el caso anterior, sea
. Siguiendo la misma línea que en el caso anterior, sea ![]() definido como en
la ec. (11). Sea
definido como en
la ec. (11). Sea
![]() y
y
![]() . Reagrupando los términos según se hizo en la ec. (12) se puede escribir
. Reagrupando los términos según se hizo en la ec. (12) se puede escribir
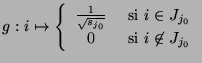
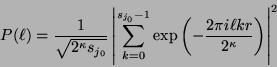
![]() es un número racional no-negativo, su fracción continuada es
es un número racional no-negativo, su fracción continuada es
![]() , se calcula su fracción continuada
, se calcula su fracción continuada
![]() (
(![]() ) y los correspondientes convergentes
) y los correspondientes convergentes
![]() (también
(también ![]() ), y entre éstos se selecciona a aquellos cuyos denominadores
), y entre éstos se selecciona a aquellos cuyos denominadores ![]() sean menores que
sean menores que ![]() , los cuales han de ser divisores del orden
, los cuales han de ser divisores del orden ![]() de
de ![]() .
.