


Posterior: Elementos con orden arbitrario
Arriba: Algoritmo cuántico para el
Anterior: Algoritmo cuántico para el
Supongamos dado 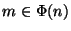 y que éste es tal que su orden
y que éste es tal que su orden 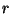 es una potencia de 2.
es una potencia de 2.
Sea
 donde
donde
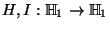 son los operadores de Hadamard e identidad respectivamente.
Por la ec. (4) se tiene
son los operadores de Hadamard e identidad respectivamente.
Por la ec. (4) se tiene
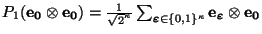 . Escribamos
. Escribamos
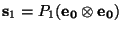 . Ahora, aplicando el operador
. Ahora, aplicando el operador 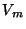 , resulta
, resulta
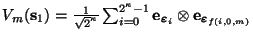 . Escribamos
. Escribamos
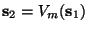 .
.
Ya que
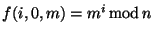 ,
, 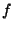 es una función periódica de período
es una función periódica de período 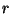 respecto a
respecto a 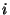 . Sea
. Sea
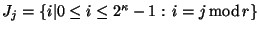 la clase de índices que dejan residuo
la clase de índices que dejan residuo 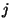 al dividírseles entre
al dividírseles entre 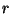 . Claramente
. Claramente
![$[\![0,2^{\kappa}-1]\!] = \bigcup_{j=0}^{r-1} J_j$](img389.png) , y la cardinalidad de cada conjunto
, y la cardinalidad de cada conjunto  es
es
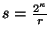 , el cual número, para este caso, es entero. Por tanto, es posible reescribir
, el cual número, para este caso, es entero. Por tanto, es posible reescribir
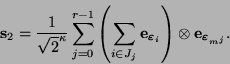 |
(12) |
Si aquí se aplica el postulado de medición, entonces se elegirá a un vector de la forma
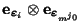 ,
,  , para una potencia fija
, para una potencia fija  , con probabilidad
, con probabilidad
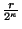 . El estado correspondiente a esta situación es de la forma
. El estado correspondiente a esta situación es de la forma
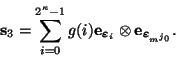 |
(13) |
donde
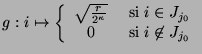
La función 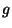 también es periódica, de período
también es periódica, de período 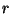 . Ahora, se tiene que la transformada de Fourier de
. Ahora, se tiene que la transformada de Fourier de 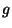 ,
, 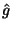 será también periódica pero de período proporcional a
será también periódica pero de período proporcional a 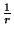 .
.
Calculemos la transformada inversa discreta de Fourier de
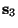 :
:
y al intercambiar el orden de las sumatorias se obtiene:
 |
(14) |
Ya que
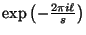 es una raíz
es una raíz 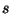 -ésima de la unidad, se tiene
-ésima de la unidad, se tiene
 será 1 o 0 en función de que
será 1 o 0 en función de que 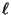 sea o no un múltiplo entero de
sea o no un múltiplo entero de 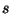 , es decir un número de la forma
, es decir un número de la forma 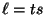 , con
, con
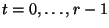 . Aquí es esencial el hecho de que
. Aquí es esencial el hecho de que 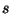 es entero. Así pues, de (14),
es entero. Así pues, de (14),
 |
(15) |
Las relaciones (13) y (15), que expresan a
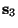 y
y
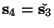 , involucran ambas al orden
, involucran ambas al orden 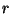 . Pero hay una diferencia esencial entre ellas: En (13) los índices
. Pero hay una diferencia esencial entre ellas: En (13) los índices 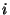 , en el primer qubit, correspondientes a coeficientes no-nulos dependen de la potencia ``aleatoria''
, en el primer qubit, correspondientes a coeficientes no-nulos dependen de la potencia ``aleatoria'' 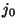 , en tanto que en (15) no dependen de ésa, e involucran sin embargo, a
, en tanto que en (15) no dependen de ésa, e involucran sin embargo, a 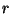 .
.
Si ahora se aplica el postulado de medición se obtendrá un valor de la forma
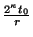 , con
, con
![$t_0\in[\![0,r-1]\!]$](img414.png) , cada uno con probabilidad
, cada uno con probabilidad 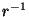 . Si
. Si 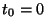 , entonces no es posible obtener ninguna información acerca de
, entonces no es posible obtener ninguna información acerca de 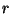 y se ha de repetir el procedimiento otra vez. En otro caso, al dividir entre
y se ha de repetir el procedimiento otra vez. En otro caso, al dividir entre 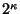 se tiene el valor racional
se tiene el valor racional
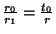 . Se conoce a
. Se conoce a  y
y 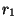 mas aún no se conoce
mas aún no se conoce 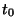 ni
ni 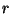 . Sin embargo, necesariamente
. Sin embargo, necesariamente 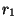 divide a
divide a 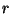 . Así pues, se puede aplicar de nuevo el algoritmo cuántico a partir de
. Así pues, se puede aplicar de nuevo el algoritmo cuántico a partir de 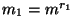 .
Procediendo recursivamente se obtiene una factorización
.
Procediendo recursivamente se obtiene una factorización
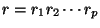 conteniendo a lo más
conteniendo a lo más 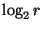 factores.
factores.
En resumen, el algoritmo para localizar divisores de órdenes de elementos es el siguiente:
- Entrada.
-
 ,
, 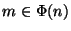 de orden potencia de 2.
de orden potencia de 2.
- Salida.
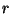 tal que
tal que  .
.
- Procedimiento
- DivisorOrdenPotencia2
- Sea
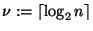 ,
, 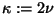 .
.
- Defínase
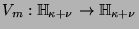 como en la ec. (11).
como en la ec. (11).
- Sea
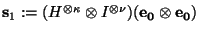 .
.
- Sea
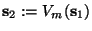 .
.
- Sea
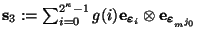 el estado equivalente a ``tomar una medición'' en
el estado equivalente a ``tomar una medición'' en
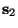 . Entonces
. Entonces 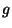 queda determinada como en la ec. (13).
queda determinada como en la ec. (13).
- Sea
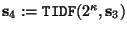 la transformada inversa discreta de Fourier de
la transformada inversa discreta de Fourier de
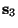 .
.
- Sea
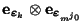 una medición de
una medición de
 .
.
- Si
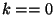 repítase desde el paso 3. En otro caso sea
repítase desde el paso 3. En otro caso sea
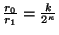 y dése como resultado
y dése como resultado 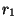 .
.
El algoritmo para calcular órdenes de elementos es el siguiente:
- Entrada.
-
 ,
, 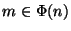 de orden potencia de 2.
de orden potencia de 2.
- Salida.
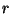 tal que
tal que 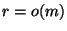 .
.
- Procedimiento
- OrdenPotencia2
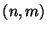
- Sean inicialmente
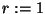 y
y 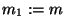 .
.
- Repítase
- sea
 ;
;
- actualícese
 ;
;
- actualícese
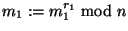 .
.
hasta tener 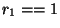 .
.
- Dése como resultado
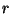 .
.



Posterior: Elementos con orden arbitrario
Arriba: Algoritmo cuántico para el
Anterior: Algoritmo cuántico para el
Guillermo Morales-Luna gmorales at cs.cinvestav.mx
2003-12-11
![]() y que éste es tal que su orden
y que éste es tal que su orden ![]() es una potencia de 2.
es una potencia de 2.
![]() donde
donde
![]() son los operadores de Hadamard e identidad respectivamente.
Por la ec. (4) se tiene
son los operadores de Hadamard e identidad respectivamente.
Por la ec. (4) se tiene
![]() . Escribamos
. Escribamos
![]() . Ahora, aplicando el operador
. Ahora, aplicando el operador ![]() , resulta
, resulta
![]() . Escribamos
. Escribamos
![]() .
.
![]() ,
, ![]() es una función periódica de período
es una función periódica de período ![]() respecto a
respecto a ![]() . Sea
. Sea
![]() la clase de índices que dejan residuo
la clase de índices que dejan residuo ![]() al dividírseles entre
al dividírseles entre ![]() . Claramente
. Claramente
![]() , y la cardinalidad de cada conjunto
, y la cardinalidad de cada conjunto ![]() es
es
![]() , el cual número, para este caso, es entero. Por tanto, es posible reescribir
, el cual número, para este caso, es entero. Por tanto, es posible reescribir
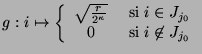
![]() también es periódica, de período
también es periódica, de período ![]() . Ahora, se tiene que la transformada de Fourier de
. Ahora, se tiene que la transformada de Fourier de ![]() ,
, ![]() será también periódica pero de período proporcional a
será también periódica pero de período proporcional a ![]() .
.
![]() :
:
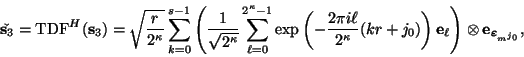
![]() , con
, con
![]() , cada uno con probabilidad
, cada uno con probabilidad ![]() . Si
. Si ![]() , entonces no es posible obtener ninguna información acerca de
, entonces no es posible obtener ninguna información acerca de ![]() y se ha de repetir el procedimiento otra vez. En otro caso, al dividir entre
y se ha de repetir el procedimiento otra vez. En otro caso, al dividir entre ![]() se tiene el valor racional
se tiene el valor racional
![]() . Se conoce a
. Se conoce a ![]() y
y ![]() mas aún no se conoce
mas aún no se conoce ![]() ni
ni ![]() . Sin embargo, necesariamente
. Sin embargo, necesariamente ![]() divide a
divide a ![]() . Así pues, se puede aplicar de nuevo el algoritmo cuántico a partir de
. Así pues, se puede aplicar de nuevo el algoritmo cuántico a partir de ![]() .
Procediendo recursivamente se obtiene una factorización
.
Procediendo recursivamente se obtiene una factorización
![]() conteniendo a lo más
conteniendo a lo más ![]() factores.
factores.