


Posterior: Evaluación de funciones booleanas
Arriba: Nociones básicas de Computación
Anterior: qubits y palabras de
Para 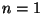 , consideraremos las siguientes compuertas básicas, llamadas también operadores cuánticos:
, consideraremos las siguientes compuertas básicas, llamadas también operadores cuánticos:
- Identidad.
-
![$I=\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]$](img153.png) .
.
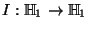 es el operador identidad.
es el operador identidad.
- Negación.
-
![$N=\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]$](img155.png) . Se tiene
. Se tiene
![$N: \left[\begin{array}{c} z_0 \\ z_1 \end{array}\right] \mapsto \left[\begin{array}{c} z_1 \\ z_0 \end{array}\right]$](img156.png) .
. 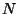 es unitaria y tiene como función permutar señales, es de hecho ``una reflexión a lo largo de la diagonal principal''.
es unitaria y tiene como función permutar señales, es de hecho ``una reflexión a lo largo de la diagonal principal''.
- Hadamard.
-
![$H=\frac{1}{\sqrt{2}}\left[\begin{array}{rr}
1 & 1 \\
1 & -1
\end{array}\right]$](img158.png) . Se tiene
. Se tiene
![$H: \left[\begin{array}{c} z_0 \\ z_1 \end{array}\right] \mapsto \frac{1}{\sqrt{2}}\left[\begin{array}{c} z_0+z_1 \\ z_0-z_1 \end{array}\right]$](img159.png) .
. 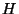 es unitaria y tiene como función ``reflejar el plano respecto al eje
es unitaria y tiene como función ``reflejar el plano respecto al eje 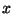 y rotar luego un ángulo de
y rotar luego un ángulo de 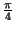 radianes, en sentido opuesto a las manecillas del reloj''.
radianes, en sentido opuesto a las manecillas del reloj''.
Naturalmente, 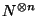 y
y 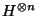 son sendas compuertas en
son sendas compuertas en  . Las matrices que las representan, respecto a la base producto
. Las matrices que las representan, respecto a la base producto
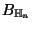 , pueden ser calculadas mediante la relación (1).
, pueden ser calculadas mediante la relación (1).
Observamos aquí, primeramente, que 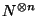 actúa como el ``complemento a
actúa como el ``complemento a 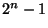 '', es decir, en los vectores básicos se tiene
'', es decir, en los vectores básicos se tiene
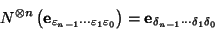 |
(3) |
donde
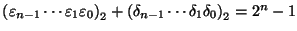 .
.
Observamos también que
y de manera general
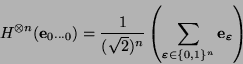 |
(4) |
es decir, el operador 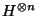 aplicado al primer vector básico
aplicado al primer vector básico
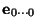 produce el estado que ````promedia'' a todos los demás con pesos uniformes''.
produce el estado que ````promedia'' a todos los demás con pesos uniformes''.
- Negación controlada.
- Sea
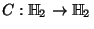 la transformación lineal que sobre los vectores básicos actúa
la transformación lineal que sobre los vectores básicos actúa
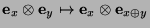 (recuerdo una vez más que
(recuerdo una vez más que 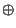 es la disyunción excluyente, o más bien la adición módulo 2). Esta transformación se llama negación controlada debido a que en su salida, el segundo qubit es la negación del primero sólo si en la entrada el segundo qubit ``estaba prendido''. Esto puede verse como que el segundo qubit de entrada sirve de ``control'' para aplicar el operador de negación al primero, el cual hace las veces de ``argumento''.
es la disyunción excluyente, o más bien la adición módulo 2). Esta transformación se llama negación controlada debido a que en su salida, el segundo qubit es la negación del primero sólo si en la entrada el segundo qubit ``estaba prendido''. Esto puede verse como que el segundo qubit de entrada sirve de ``control'' para aplicar el operador de negación al primero, el cual hace las veces de ``argumento''.
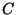 no es el producto tensorial de dos transformaciones unitarias en
no es el producto tensorial de dos transformaciones unitarias en 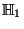 . Se tiene que
. Se tiene que 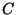 queda representado, respecto a la base canónica de
queda representado, respecto a la base canónica de 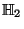 por la matriz
por la matriz
- Negación controlada cambiada.
- Sea
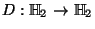 la transformación lineal tal que
la transformación lineal tal que
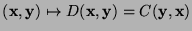 que tan sólo cambia los roles de variable de control y variable de argumento. Se tiene
que tan sólo cambia los roles de variable de control y variable de argumento. Se tiene
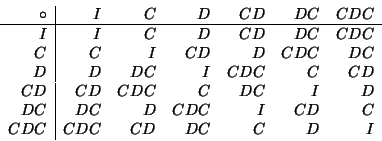
En el espacio de transformaciones unitarias, 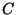 y
y 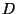 generan un subgrupo con la operación de composición. La tabla de multiplicación del subgrupo es de la forma:
generan un subgrupo con la operación de composición. La tabla de multiplicación del subgrupo es de la forma:
Alternativamente, podemos decir que este grupo queda presentado por su unidad 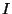 , dos generadores
, dos generadores 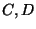 y la relación
y la relación 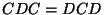 . De hecho este grupo es isomorfo al grupo de permutaciones de 3 elementos,
. De hecho este grupo es isomorfo al grupo de permutaciones de 3 elementos, 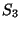 . En efecto, si
. En efecto, si 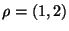 es la reflexión y
es la reflexión y  es el ciclo de orden 3, entonces se puede identificar
es el ciclo de orden 3, entonces se puede identificar
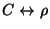 ,
,
 .
.
- Reversos.
- Entre los elementos que aparecen en el ejemplo anterior,
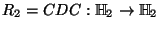 queda representado, respecto a la base canónica, mediante la matriz
queda representado, respecto a la base canónica, mediante la matriz
es decir, es tal que
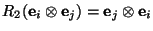 . De hecho, para cada
. De hecho, para cada 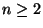 , actuando sobre la base canónica, se tiene:
, actuando sobre la base canónica, se tiene:
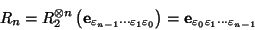 |
(5) |
es decir, el efecto de este operador es revertir el orden de la ``palabra de entrada'', por lo cual, 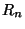 se dice ser el operador reverso.
se dice ser el operador reverso.
Un estado en  , digamos
, digamos
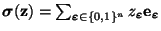 está determinado por las
está determinado por las 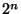 coordenadas del vector
coordenadas del vector
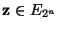 . Si
. Si
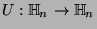 es una compuerta cuántica, el estado
es una compuerta cuántica, el estado
 al que arriba al aplicársele el operador
al que arriba al aplicársele el operador 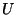 consta también de
consta también de 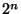 coordenadas. De esta manera, un cálculo que involucra un número exponencial de términos se hace en ``un paso'' de cómputo cuántico y es posible así acelerar el proceso de corrida.
coordenadas. De esta manera, un cálculo que involucra un número exponencial de términos se hace en ``un paso'' de cómputo cuántico y es posible así acelerar el proceso de corrida.
Toda combinación lineal de elementos en la base cuyos coeficientes formen un punto en la esfera euclidiana unitaria de
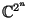 es un estado,
es un estado,
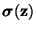 . Se dice que el estado es descomponible, o factorizable, si es de la forma
. Se dice que el estado es descomponible, o factorizable, si es de la forma
 , con
, con
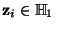 . Un estado que no es descomponible se dice ser revuelto (entangled state).
. Un estado que no es descomponible se dice ser revuelto (entangled state).



Posterior: Evaluación de funciones booleanas
Arriba: Nociones básicas de Computación
Anterior: qubits y palabras de
Guillermo Morales-Luna gmorales at cs.cinvestav.mx
2003-12-11
![]() , consideraremos las siguientes compuertas básicas, llamadas también operadores cuánticos:
, consideraremos las siguientes compuertas básicas, llamadas también operadores cuánticos:
![$I=\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]$](img153.png) .
.
![$N=\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]$](img155.png) . Se tiene
. Se tiene
![$N: \left[\begin{array}{c} z_0 \\ z_1 \end{array}\right] \mapsto \left[\begin{array}{c} z_1 \\ z_0 \end{array}\right]$](img156.png) .
. ![$H=\frac{1}{\sqrt{2}}\left[\begin{array}{rr}
1 & 1 \\
1 & -1
\end{array}\right]$](img158.png) . Se tiene
. Se tiene
![$H: \left[\begin{array}{c} z_0 \\ z_1 \end{array}\right] \mapsto \frac{1}{\sqrt{2}}\left[\begin{array}{c} z_0+z_1 \\ z_0-z_1 \end{array}\right]$](img159.png) .
. ![]() actúa como el ``complemento a
actúa como el ``complemento a ![]() '', es decir, en los vectores básicos se tiene
'', es decir, en los vectores básicos se tiene
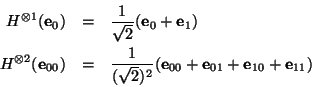
![]() no es el producto tensorial de dos transformaciones unitarias en
no es el producto tensorial de dos transformaciones unitarias en ![]() . Se tiene que
. Se tiene que ![]() queda representado, respecto a la base canónica de
queda representado, respecto a la base canónica de ![]() por la matriz
por la matriz
![\begin{displaymath}C=\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 %%\\
\end{array}\right]\end{displaymath}](img178.png)
![\begin{displaymath}D=\left[\begin{array}{cccc}
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 %%\\
\end{array}\right]\end{displaymath}](img181.png)
![\begin{displaymath}R_2=\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 %%\\
\end{array}\right],\end{displaymath}](img193.png)
![]() , digamos
, digamos
![]() está determinado por las
está determinado por las ![]() coordenadas del vector
coordenadas del vector
![]() . Si
. Si
![]() es una compuerta cuántica, el estado
es una compuerta cuántica, el estado
![]() al que arriba al aplicársele el operador
al que arriba al aplicársele el operador ![]() consta también de
consta también de ![]() coordenadas. De esta manera, un cálculo que involucra un número exponencial de términos se hace en ``un paso'' de cómputo cuántico y es posible así acelerar el proceso de corrida.
coordenadas. De esta manera, un cálculo que involucra un número exponencial de términos se hace en ``un paso'' de cómputo cuántico y es posible así acelerar el proceso de corrida.
![]() es un estado,
es un estado,
![]() . Se dice que el estado es descomponible, o factorizable, si es de la forma
. Se dice que el estado es descomponible, o factorizable, si es de la forma
![]() , con
, con
![]() . Un estado que no es descomponible se dice ser revuelto (entangled state).
. Un estado que no es descomponible se dice ser revuelto (entangled state).