



Siguiente: PB visto como un
Un nivel arriba: Expresiones regulares y sistemas
Anterior: Introducción
Consideremos n bloques, enumerados con los números
naturales
![$\mbox{\bf n}=[1, 2, \ldots, n]$](img1453.gif) .
Asociémosle al piso el número 0. El mundo es
.
Asociémosle al piso el número 0. El mundo es
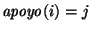 .
En cada estado, o configuración del universo, tendremos un cierto
número de columnas, cada una de ellas constituída por
bloques apilados. Ya que cada bloque está bien sobre el piso o
bien sobre algún otro bloque, a cada configuración podemos asociarle una función
.
En cada estado, o configuración del universo, tendremos un cierto
número de columnas, cada una de ellas constituída por
bloques apilados. Ya que cada bloque está bien sobre el piso o
bien sobre algún otro bloque, a cada configuración podemos asociarle una función
 .
Naturalmente, si
.
Naturalmente, si
 tendremos que el bloque
i está sobre el objeto j. Así pues,tendremos las siguientes
propiedades para una tal función apoyo:
tendremos que el bloque
i está sobre el objeto j. Así pues,tendremos las siguientes
propiedades para una tal función apoyo:
- 1.
- ``Sólo el piso puede ser apoyo de más de un bloque''. En símbolos
- 2.
- ``El número de columnas en un estado coincide con el de
bloques apoyados en el piso''. En símbolos:
- 3.
- ``Las columnas no son aros''. En símbolos:
- 4.
- ``Cada columna tiene una base en el piso''. En símbolos:
- 5.
- ``Cada bloque está sobre su apoyo''. En símbolos:
Los estados del universo corresponden de manera biunívoca con las funciones de apoyo. Por tanto, contar los posibles estados en el PB equivale a contar las funciones de apoyo.
Sea pues
Para una función
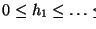 ,
sea k el número de columnas que define y
,
sea k el número de columnas que define y
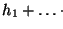 sea hj el número de bloques en la columna j-ésima. Supondremos a las
columnas ordenadas de manera no-decreciente en cuanto a sus
alturas. Entonces tendremos que
sea hj el número de bloques en la columna j-ésima. Supondremos a las
columnas ordenadas de manera no-decreciente en cuanto a sus
alturas. Entonces tendremos que
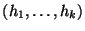 y
además
y
además
 .
En este sentido, diremos que el
estado determina a la sucesión
.
En este sentido, diremos que el
estado determina a la sucesión
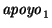 .
Surge pues la necesidad de analizar al conjunto de sucesiones
.
Surge pues la necesidad de analizar al conjunto de sucesiones
Observamos que dos estados
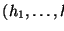 y
y
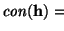 determinan a una misma sucesión
determinan a una misma sucesión
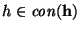 si y
sólo si el estado
si y
sólo si el estado
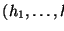 difiere del estado
difiere del estado
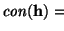 tan sólo por una permutación de los n bloques en el Mundo. Tenemos n! permutaciones tales.
Ahora, para una sucesión
tan sólo por una permutación de los n bloques en el Mundo. Tenemos n! permutaciones tales.
Ahora, para una sucesión
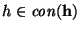 podemos tener varias de sus entradas iguales, en otras palabras, en cada estado que determine a la sucesión, varias de sus columnas pueden tener una misma altura.
Tomemos pues el conjunto de valores distintos que aparecen en
ella. Sea éste
podemos tener varias de sus entradas iguales, en otras palabras, en cada estado que determine a la sucesión, varias de sus columnas pueden tener una misma altura.
Tomemos pues el conjunto de valores distintos que aparecen en
ella. Sea éste
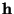 .
Para cada
.
Para cada
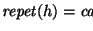 ,
contemos sus repeticiones en
,
contemos sus repeticiones en
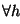 ,
sea pues
,
sea pues
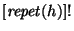 .
Convengamos también en
identificar columnas de igual tamaño. De esta manera,
.
Convengamos también en
identificar columnas de igual tamaño. De esta manera,
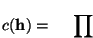 ,
,
![$\left[\mbox{\it repet\/}( h )\right]!$](img1477.gif) permutaciones de columnas de altura h quedarán identificadas. Luego, habrá
permutaciones de columnas de altura h quedarán identificadas. Luego, habrá
![$c(\mbox{\bf h}) = {\displaystyle \prod_{h \in \mbox{\it con\/}( \mbox{\bf h} )}\left[\mbox{\it repet\/}( h )\right]!}$](img1478.gif) estados
identificados, cada uno de los cuales determina a la sucesión
estados
identificados, cada uno de los cuales determina a la sucesión
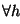 .
Hechas las observaciones anteriores, un minuto de reflexión
basta para convencerse de que vale la relación siguiente:
.
Hechas las observaciones anteriores, un minuto de reflexión
basta para convencerse de que vale la relación siguiente:
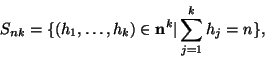 |
(44) |
Pasemos ahora a encontrar una expresión equivalente cuya
evaluación sea más sencilla.
Dados n > 1 y 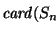 ,
¿de cuántas formas podemos
expresar a n como una suma de k sumandos enteros positivos?. En
otras palabras, si definimos
,
¿de cuántas formas podemos
expresar a n como una suma de k sumandos enteros positivos?. En
otras palabras, si definimos
¿cuál es la cardinalidad de Snk?
Observemos que, en su representación unaria, n se escribe
como una sarta de n 1's, es decir, como n ``palitos contiguos''. En
esa sarta tendremos n-1 separaciones entre palitos adyacentes. Si
elegimos a k-1 de tales separaciones para introducir otras tantas
marcas separadoras, los n palitos quedarán agrupados en k hatos contiguos, cada uno con al menos un palito, y la suma de todos
ellos nos da, en efecto, los n palitos. Así pues, tendremos
que
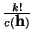 .
Ahora, cada sucesión
.
Ahora, cada sucesión
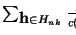 tiene a sus entradas ordenadas de manera no-decreciente. Si omitimos esta exigencia de orden, un segundo minuto de reflexión nos convencerá de que la sucesión
tiene a sus entradas ordenadas de manera no-decreciente. Si omitimos esta exigencia de orden, un segundo minuto de reflexión nos convencerá de que la sucesión
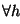 dará origen a
dará origen a
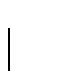 elementos distintos en Snk. Al conjuntar estas dos observaciones,
tenemos que
elementos distintos en Snk. Al conjuntar estas dos observaciones,
tenemos que
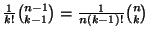 y consecuentemente
y consecuentemente
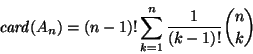 |
(45) |
Una mera manipulación algebraica da
 .
Así pues, logramos nuestro objetivo al sustituir 4.34 en
4.33:
.
Así pues, logramos nuestro objetivo al sustituir 4.34 en
4.33:
Lo que equivale a que
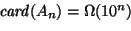 |
(46) |
Esta última relación nos da la naturaleza explosiva del
PB. En la Tabla 4.3 presentamos algunos números de estados resultantes con diversos números de bloques.
Table 4.3:
Estados en el PB en función de los bloques.
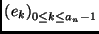 |
Se ve que
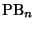 .
Este crecimiento rápido del número de estados es lo que, en la práctica, hace
intratable al PB con este enfoque. Sin embargo, aún nos dedicaremos a él para ilustrar el uso de expresiones regulares.
.
Este crecimiento rápido del número de estados es lo que, en la práctica, hace
intratable al PB con este enfoque. Sin embargo, aún nos dedicaremos a él para ilustrar el uso de expresiones regulares.




Siguiente: PB visto como un
Un nivel arriba: Expresiones regulares y sistemas
Anterior: Introducción
Guillermo Morales-Luna
2000-06-27
 .
Naturalmente, si
.
Naturalmente, si
 tendremos que el bloque
i está sobre el objeto j. Así pues,tendremos las siguientes
propiedades para una tal función apoyo:
tendremos que el bloque
i está sobre el objeto j. Así pues,tendremos las siguientes
propiedades para una tal función apoyo:
 .
En este sentido, diremos que el
estado determina a la sucesión
.
En este sentido, diremos que el
estado determina a la sucesión
![$\left[\mbox{\it repet\/}( h )\right]!$](img1477.gif) permutaciones de columnas de altura h quedarán identificadas. Luego, habrá
permutaciones de columnas de altura h quedarán identificadas. Luego, habrá
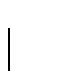 elementos distintos en Snk. Al conjuntar estas dos observaciones,
tenemos que
elementos distintos en Snk. Al conjuntar estas dos observaciones,
tenemos que
 .
Así pues, logramos nuestro objetivo al sustituir 4.34 en
4.33:
.
Así pues, logramos nuestro objetivo al sustituir 4.34 en
4.33:
