



Siguiente: Minimización de autómatas
Un nivel arriba: Expresiones regulares y sistemas
Anterior: El mundo de los
Sea n > 1. Sea
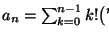 el conjunto de estados correspondientes al PB con n bloques,
el conjunto de estados correspondientes al PB con n bloques,
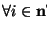 .
Según vimos anteriormente
.
Según vimos anteriormente
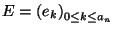 .
.
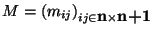 codificaremos a la
instrucción ``Colóquese el bloque i sobre el objeto j'' mediante un símbolo especial mij. Claramente, un tal símbolo mij
sólo podrá aplicarse a un estado ek cuando en este estado ni i
ni j tienen un bloque encima, a menos que j = 0, es decir, que el
objeto j sea precisamente el piso. Introduzcamos entonces un
estado más, ean, de inconsistencia. Sea pues
codificaremos a la
instrucción ``Colóquese el bloque i sobre el objeto j'' mediante un símbolo especial mij. Claramente, un tal símbolo mij
sólo podrá aplicarse a un estado ek cuando en este estado ni i
ni j tienen un bloque encima, a menos que j = 0, es decir, que el
objeto j sea precisamente el piso. Introduzcamos entonces un
estado más, ean, de inconsistencia. Sea pues
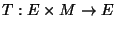 el conjunto de estados y sea
el conjunto de estados y sea
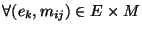 el conjunto de símbolos del autómata correspondiente al
el conjunto de símbolos del autómata correspondiente al
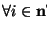 .
Las
transiciones en él, estarán dadas por la función
.
Las
transiciones en él, estarán dadas por la función
 tal que
tal que
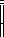 ,
T(ek, mij) es bien el estado de inconsistencia ean, en el caso que mij no pueda aplicarse
a ek, o bien es el estado que difiere de ek tan sólo por la
aplicación del movimiento mij a ek, cuando ésta es posible.
A guisa de ejemplos, en las tablas 4.4 y 4.5 mostramos las tablas de transición de los autómatas correspondientes a 2 y 3 bloques respectivamente.
,
T(ek, mij) es bien el estado de inconsistencia ean, en el caso que mij no pueda aplicarse
a ek, o bien es el estado que difiere de ek tan sólo por la
aplicación del movimiento mij a ek, cuando ésta es posible.
A guisa de ejemplos, en las tablas 4.4 y 4.5 mostramos las tablas de transición de los autómatas correspondientes a 2 y 3 bloques respectivamente.
Table 4.4:
Matriz de transición del autómata correspondiente a 2 bloques.
 |
Table 4.5:
Matriz de transición del autómata correspondiente a 3 bloques.
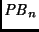 |
Ahora, para el (semi-)autómata
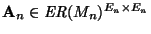 correspondiente a
correspondiente a
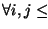 consideremos la matriz
consideremos la matriz
 tal que
tal que
 :
:
Para dos bloques, se tiene
Para dos bloques, se tiene la matriz de la tabla 4.6.
Table 4.6:
Matriz de coeficientes del sistema de derivadas.
![\begin{table}\begin{displaymath}\mbox{\bf A}_3=\left[\mbox{\bf A}_{31}\; \mbox{\...
...{23}+m_{30}+m_{31}+m_{32}
\end{array}\right]
\end{eqnarray*}}
\end{table}](img1508.gif) |
Para
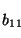 se puede calcular su potencia ``estrella'' por el algoritmo descrito anteriormente. Se obtiene que
se puede calcular su potencia ``estrella'' por el algoritmo descrito anteriormente. Se obtiene que
donde
Hemos visto que en teoría es posible utilizar los
algoritmos presentados, relativos a los autómatas finitos, para
encontrar a todos los posibles planes para pasar de un estado a
otro en el Mundo de los Bloques y resolver así cualquier
instancia del PB. En la práctica, hemos visto que, incluso para
el caso trivial de sólo dos bloques, la solución con este
enfoque es difícil. De hecho, la complejidad de este algoritmo
crece notablemente, en tiempo y en espacio, con el número n de
bloques considerados.




Siguiente: Minimización de autómatas
Un nivel arriba: Expresiones regulares y sistemas
Anterior: El mundo de los
Guillermo Morales-Luna
2000-06-27
 tal que
tal que
 tal que
tal que
 :
: