- 1.
- L es regular.
- 2.
- L es la unión de algunas clases de equivalencia de una relación de equivalencia de índice finito, congruente por la derecha con la concatenación de palabras.
- 3.
- La relación
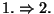 tal que
tal que
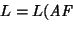
es una relación de índice finito.
 Supongamos L regular. Sea
Supongamos L regular. Sea
 .
Consideremos la función
.
Consideremos la función
 se tiene que
se tiene que
![$\mbox{\it tran\/}:([\sigma],e)\mapsto [\sigma e]$](img1535.gif) .
Es evidente que una palabra es reconocida por
.
Es evidente que una palabra es reconocida por
 son indistinguibles si para cualquier palabra
son indistinguibles si para cualquier palabra
 no fueran indistinguibles, entonces habría una palabra
no fueran indistinguibles, entonces habría una palabra
 incluyamos la pareja
incluyamos la pareja