T3 mosaic

Figure 1.10: The plane tiled by T3 triangles. Left: alpha phase, in which the triangles are stacked diagonally with slope -1/2 in periodic rectangular tiles 7x14. Right: preferred ethereal beta phase, in which they are stacked diagonally with slope -2 in periodic rectangular tiles 14x7. The beta phase welcomes intercalcated T1's, whereas the alpha phase does not,

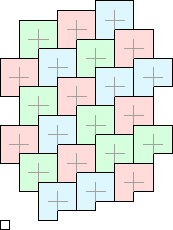
Continuing, there are two tilings by T3's, likewise designated alpha and beta phases. Both string their tiles along diagonals, as shown in Figure 1.10, The tile to the right sits higher in the alpha phase than in the beta phase, these two diagonal positions being the only ones compatible with Rule 110. Trying to stack T3's in a vertical column would lead to the combination for which Rule 102 was rejected.

Of these two enantiomers (yes, one is a mirror reflection of the other, in the diagonal), the beta form is ubiquitous in evolutions, constituting Cook's ether. It easily combines with other tiles; two mixtures with T1's give the two simplest gliders, designated A and B. By itself it covers the plane with a density of 57%.

Figure 1.11: Left and Right: the two enantiomers of the T3 tile. Center: The T3 can combine with a T1 to produce a hexagonal lattice with a larger unit cell than T3 alone. Only one of the two enantiomers is shown.

Rule 110 has a predisposition toward the planar hexagonal lattice, on account of the domination of the evolution by upside down isosceles right triangles. On the other hand, the simple mosaics, while clearly displaying the hexagonal format, all differ in the size and orientation of the principal axes since they depend on triangles of different sizes.

The $14x7$ unit crystallographic cell for the ether lattice was noted by Lind [9], and evidently has a more convenient periodicity than does the alpha variant. Whatever the reason, the beta version is overwhelmingly preferred as the eventual destination of long term evolution from random initial configurations. One good reason for the asymmetry lies in the packing of T1's with T3's. T1's and T3's have the same symmetry, but the diagonally reflected T1 lattice is incompatible with the rule of evolution; indeed alternate rows belong to the Garden of Eden.

The discrepancy consists in the fact that T1's can, and often are, stacked vertically, but in the mirror reflection they would have to run along horixontally, violating the abuttment proscription. Consequently, since columns of T1's often occur in Rule 110 gliders, no enantiomer of a glider with too long a vertical stack would exist.

Figure 1.12: The ether lattice is a mosaic of slightly squished hexagons. In common with hexagonal lattices it can be decomposed into three sublattices each of which can be assigned one of three different colors.