ether crystallography

Figure 1.13: The locations of Cook's gliders relative to the ether lattice. The two barred gliders sit lower on the same velocity lines as the unbarred gliders. Small circles on the T3 mosaic show possible positions of compatible gliders, but they could be impossible, duplicates, or so far undiscovered.

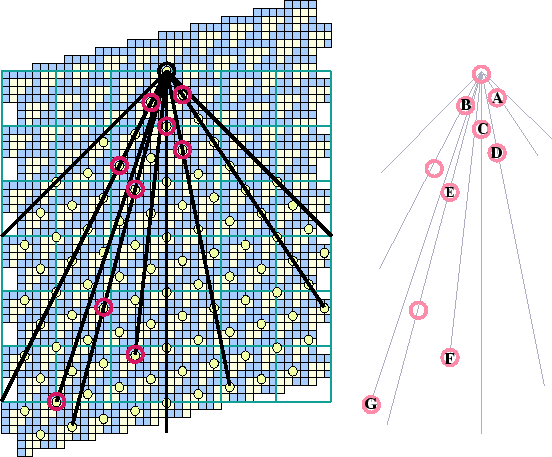
By definition, mosaics define crystallographic lattices, relative to which eventual gliders can be seen as dislocations or other defects. Figure 1.13 shows the ether mosaic, together with the position of the light conelight cone and the locations of some of Cook's gliders. The slope of the line connecting any of them to the origin reveals the velocity of the glider. Conversely, these crystallographic faces determine possible velocities whereby it appears that the simpler combinations have already been discovered.

Table 1.1: Left: Cook's glider list, including Lind's gliders. Right: Some potential glider velocities, arranged by denominator.

designation	shift	generation
A	2	3
B	-2	4
B-bar	-6	12
C	0	7
D	2	10
E	-4	15
E-bar	-8	30
F	-4	36
G	-14	42
H	-18	92
glider	.	77

left	generation	right
	3	2
-2	4
	6	4
	7	0
-4	8
-8	9	6
	10	2
-2	11
-6	12	8
-10	13	4
	14	0	14
-4	15	10
-8	16	6

In every generation there are lattice vectors connecting congruent points in the lattice. Those with less than (or exactly) light velocity are listed in Table 1.1, for the first sixteen generations. Note that such combinations as two in three generations and four in six generations refer to the same velocity, but not necessarily the same gliders. Sometimes additional time is required to develop a cycle fully. Of course any gliders obeying $m$ in $n$ will also obey $km$ in $kn$. Gliders can appear for the first time when $k = 2$ which were absent for $k = 1$; it is more usual that all the old ones remain and either new ones arise, or new interconnections develop between the old ones. And, of course, the value of $k$ can sometimes make no difference, and no gliders may exist at a velocity which otherwise seems reasonable.