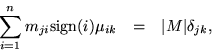Antisymmetric multilinear functions

The contrasting property to symmetry is antisymmetry which, for a function of two interchangeable variables, would read:

$$\begin{eqnarray*} f(x, y) & = & - f(y,x). \end{eqnarray*}$$

Among the most visible changes would be the result $f(x, x) = 0$, with corresponding changes in its matrix representation with respect to a basis:

$$\begin{eqnarray*} f(a e_1 + b e_2, c e_1 + d e_2) & = & \left[ \begin{array}[... ...right] \left[ \begin{array}{l} c \\ d \end{array} \right], \end{eqnarray*}$$

If the dimension of the space were larger, the dimension of the metric matrix would increase accordingly, although it would always be antisymmetric. The resulting geometry would be of a different kind, usually called symplecticsymplectic, with interesting and characteristic properties of its own.

Alternating multilinear functions provide the abstract setting, based on linear algebra, within which to discuss objects such as determinants, minors, cofactors and a vaiety of vector products, which became well established in the applications of algebra long before the axiomatic point of view arose. Determinants, for which the number of arguments matches their dimension, are the outstanding example of the unifying approach, serving as a prototype for the study of the remainder of these functions. Its requirements are:

1. $f$ is linear in each argument, the remaining arguments held constant,
2. $f$ changes sign whenever a pair of arguments are exchanged,
3. the value assigned to a basis (with its vectors listed in order) is 1.

The third principle simply provides a normalization factor; if another function $g$ follows the first two axioms but not the third, it will have the same value as $f$, but multiplied by $g$ applied to the basis.

Figure: A Determinant referred to a Basis. The right triangles can be rearranged to show that the area of the parallelogram is $(ad-bc)$.

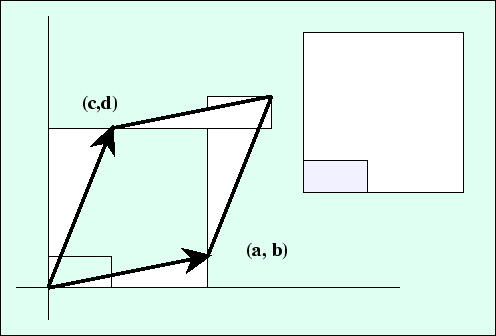In two dimensions the formula above reduces to the familiar $(ad-bc)$; in $n$ dimensions, the same process obligingly yields the traditional signed sum of permuted products. It is only necessary to expand all the vectors according to a basis, usually the coordiate basis itself, change signs to put the basis vectors in order, and elimate any terms with repetitions. The result is a sum over permutations,

$$\begin{eqnarray*} \vert M\vert & = & \sum_{permutations\ \pi} {\rm sign}(\pi)\prod_{i=1}^n m_{i\pi(i)}, \end{eqnarray*}$$

where the traditional symbol $\vert M\vert$ has been used for the determinant of the matrix $M$.

A less ambitions decomposition leads to Laplace's expansionLaplace's expansion; for example, write

$$\begin{eqnarray*} \vert M\vert & = & \sum_{i=1}^n m_{i1}\vert e_i,X_2,X_3,\ldots,X_n\vert. \end{eqnarray*}$$

Naturally, any column other than the first could have been chosen, at the cost of writing a messier formula.

Having applied the determinant formula to the summands, zeroes and ones will occur here and there because of the components of the constant vectors $E_i$. The resulting formulas can be simplified by observing that they refer to new determinants, gotten from the old by crossing out the first column and the $i^{th}$ row of $M$. Those are the minorsminor of $\vert M\vert$, say $\mu_{i1}$. In fuller generality, had the $j^{th}$ column been used instead of the first,

$$\begin{eqnarray*} \vert M\vert & = & \sum_{i=1}^n m_{ji}\mu_{ij}, \end{eqnarray*}$$

and the transposition of the subscripts between $m$ and $\mu$ is quite correct.

In fact, if a wrong row of $\mu$'s were placed in this formula, it would describe a determinant in which a wrong column had been repeated twice; once where it belongs and once where the $j^{th}$ column of $M$ ought to have been. Far from being an annoying mistake, the substitution can be exploited to obtain the inverse of $M$. Under this interpretation,

$$\begin{eqnarray*} \sum_{i=1}^n m_{ji}{\rm sign}(i)\mu_{ik} & = & \vert M\vert\delta_{jk}, \end{eqnarray*}$$

Signed minors are called cofactorscofactor, whilst the matrix of cofactors is called the adjugateadjugate of $M$, written $M^A$. Since these equations state that

$$\begin{eqnarray*} M M^A & = & \vert M\vert I, \end{eqnarray*}$$

the inverse of $M$ is

$$\begin{eqnarray*} M^{-1} & = & \frac{1}{\vert M\vert} M^A \end{eqnarray*}$$

whenever its determinant is nonzero. Otherwise there is no inverse and the adjugate contains columns annihilated by M.