Using determinants

If an ordered set of edges is given the sign of its handedness, it is not so hard to associate determinants with the volume (or area, as the case may be) of the parallelopiped whose edges are the columns of the determinant. Or its rows, for that matter. Multilinearity is a consequence of volume being base times height. Change of sign follows from changing the handedness of the edges, and a unit cube is always assigned unit volume. In fact, if the multilinearity is supposed to apply to negative (reversed direction) vectors as well as positive vectors (which it must, for arithmetic consistency), and repeating two arguments (``flatness'') gives zero volume, then $f(x - y, x - y) = 0$ implies $f(x, y) + f(y, x) = 0$, and the alternate attribute of $f$ is a direct consequence.

The vanishing of a determinant is a good way to detect linear dependence; When one vector is a combination of the others, the altitude which it should carry is zero. Likewise, there should be some other vector perpendicular (measured by the inner product) to all the vectors of the determinant.

To see how nicely recourse to the axioms sometimes shortens proofs, consider the proposition that the determinant of a product is a product of determinants; at least when all the matrices are square and the determinant makes sense. Let $P$ be one matrix, $Q$ another, and consider the product $PQ$. Partition $Q$ so that it is a row of columns, and note that, as a function of Q,

$$\begin{eqnarray*} \vert P Q \vert & = & \vert{P X_1, P X_2, \ldots , P X_n}\vert \end{eqnarray*}$$

But,

$$\begin{eqnarray*} \vert{P (a X + b Y), P X2, \ldots }\vert & = & \vert{a P X + ... ... \vert{P e_1, P e_2, \ldots , P e_n.}\vert & = & \vert P \vert. \end{eqnarray*}$$

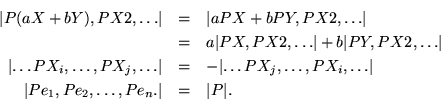
Therefore, $\vert P Q \vert = \vert P \vert \vert Q \vert$, whose vanishing, incidentally, requires that at least one factor vanish.

A longer calculation is required to show that the determinant of a matrix is the same as that of its transpose, but it does not have to be carried out in detail. Simply note that the axioms for a determinant could just as easily be stated in terms of rows as for columns, and that the only difference in the explicit formula could be expressed by writing $m_{\pi(i)i}$ instead of $m_{i\pi(i)}$. Since permutations, by definition, are one-to-one and onto, the same sum results, signs and everything. Thus its rows and columns can be exchanged without altering the value of a determinant.

The vanishing of a determinant can be used to check for linear dependence even in the absence of an explicit basis. Suppose that the vectors are $X_i$; make up a matrix $M$ using them for columns, which will have to be rectangular. Whence there must be a vector $X$, expressing the linear dependence via $M X = 0$. The determinant

$$\begin{eqnarray*} \vert M^T M\vert & = & \left[ \begin{array}{ccc} (X_1, X_1)... ..._2) & \ldots \\ \ldots & \ldots & \ldots \end{array} \right] \end{eqnarray*}$$

is called the Gram determinantGram determinant (of the Gram matrix, naturally), can only be factored when M is square, but nevertheless always vanishes according to linear dependence or not. Note that it could be the metric matrix of the subspace of the $X_i$'s.