In fact, ![]() ; the last equation of the series, asserts that
; the last equation of the series, asserts that ![]() , a proposition generally known as the Cayley-Hamilton TheoremCayley-Hamilton Theorem: a matrix satisfies its own characteristic equation.
, a proposition generally known as the Cayley-Hamilton TheoremCayley-Hamilton Theorem: a matrix satisfies its own characteristic equation.
If the factors of the characteristic polynomial are known, say by having evaluated the characteristic determinant and having found its roots, the matrix polynomial could be factored:
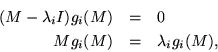
If all the eigenvalues of ![]() were distinct, there would only be one eigenvector for each eigenvalue, aside from a scalar multiplier. Therefore, using Dirac's bra and ket notationbras and kets, and observing that all the rows of
were distinct, there would only be one eigenvector for each eigenvalue, aside from a scalar multiplier. Therefore, using Dirac's bra and ket notationbras and kets, and observing that all the rows of ![]() would be proportional, just as all the columns would have
to manifest their dependence, one could deduce that
would be proportional, just as all the columns would have
to manifest their dependence, one could deduce that ![]() was proportional to
was proportional to