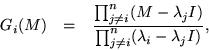
By far the best approach to constructing such a table is to observe that the gee's are Lagrange interpolation polynomials without their normalization factor (which was provided by the inner product in the denominator in the column by row formulation), with which they ought to be given for the sake of greater consistency. Doing so, one gets
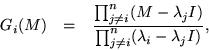
Once this detail is accommodated, the Gee's are equal to their own square, leaving a multiplication table resembling a unit matrix. The Lagrange
polynomials intervene directly in the verification of the table, without having to look at the Gee's in detail, because they are completely defined by their values over a set of distinct points. Multiplying basis polynomials taking values of zero or unity leads to similar polynomials. If at least one of the two factors contributes a zero everywhere, the product must be the constant zero. That is just what happens when ![]() contributes the factor which
contributes the factor which ![]() was lacking to complete the characteristic polynomial.
was lacking to complete the characteristic polynomial.
On the other hand, if both factors take the value ![]() in the same places, the
product still takes the value
in the same places, the
product still takes the value ![]() , so the polynomial is the same, relative to
the characteristic polynomial. It is even true that
, so the polynomial is the same, relative to
the characteristic polynomial. It is even true that
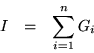
Not only can the constant function ![]() be interpolated, but also the identity
function
be interpolated, but also the identity
function ![]() , in the form
, in the form
![\begin{eqnarray*}
f(M) & = & \sum{f( \lambda_i) G_i(M) }, \\
M^{-1} & = & \sum{ \lambda_i^{-1} G_i(M) },\ \left[\lambda_i\ {\rm nonzero}\right].
\end{eqnarray*}](img156.gif)
The function formula even gives a mechanism for calculating square roots, at least for matrices with nonnegative eigenvalues. Such a quantity is required to map a matrix symmetrically into its transpose: