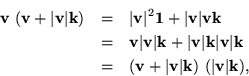To find an eigenvector with respect to quaternion multiplication, consider that ![]() commutes with all quaternions, so adding or subtracting a scalar will only add or subtract from any eigenvalue, leaving the task of diagonalizing the vector part of the quaternion. In turn, a scalar factor of the vector will only
multiply the eigenvalues by that factor, so the real task is finding eigenvectors of unit vectors - those of norm
commutes with all quaternions, so adding or subtracting a scalar will only add or subtract from any eigenvalue, leaving the task of diagonalizing the vector part of the quaternion. In turn, a scalar factor of the vector will only
multiply the eigenvalues by that factor, so the real task is finding eigenvectors of unit vectors - those of norm ![]() or norm
or norm ![]() (and those of norm
(and those of norm ![]() , for completeness). The eigenvalues of unit vectors had better be
, for completeness). The eigenvalues of unit vectors had better be ![]() , those of norm
, those of norm ![]() had better be
had better be ![]() , and those of the null vectors,
, and those of the null vectors, ![]() .
.
Unit vector or not, we have two expressions, according to sign
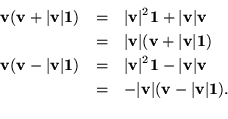
Although these formulae give eigenmatrices, the matrices are singular, containing each eigencolumn twice, each eigenrow twice. It would be nice to get one of each, and both in the same matrix. Try