vector exponential

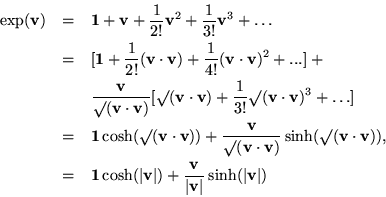
All this introduction may look tedious, but its reward is to be found in the elegance and beauty of the exponential of a vector, defined according to the traditional power series.

$$\begin{eqnarray*} \exp( {\bf v}) & = & {\bf 1}+ {\bf v}+ \frac{1}{2!}{{\bf v}}^... ...rt) + \frac{{\bf v}}{\vert{\bf v}\vert} \sinh(\vert{\bf v}\vert) \end{eqnarray*}$$

generalizing Euler's formula. The exponential of a quaternion is not much more complicated, since any scalar which could be added would commute with the quaternion, so its exponential could just be set aside as a multiplying scalar factor. How much to set aside in the general case depends on satisfying the identity $\cosh^2(x) - \sinh^2(x) = 1$, but in general there is much to be said in favor of working with vectors of unit norm and treating norms separately.

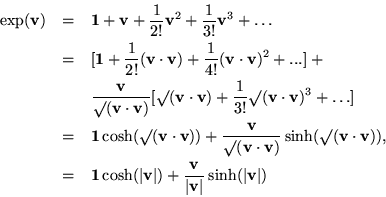
So, where is all that beauty? In great part, it lies in the law of exponents. Notice that the angle, $\surd({\bf v}\cdot{\bf v})$, is the norm of ${\bf v}$, and that imaginary quantities can be avoided by using trigonometric functions, such as should be done in association with the quaternion ${\bf i}$.

Consider, for unit vectors ${\bf u}$ and ${\bf v}$,

$$\begin{eqnarray*} \exp(\alpha {\bf u}) \exp (\beta {\bf v}) & = & ( {\bf 1}\c... ...+ \\ & & ({\bf u}\times {\bf v}) \sinh(\alpha) \sinh(\beta), \end{eqnarray*}$$

and the prospects for seeing this as

$$\begin{eqnarray*} \exp(\gamma {\bf w}) & = & {\bf 1}\cosh(\gamma) + {\bf w}\sinh(\gamma). \end{eqnarray*}$$

Just define a new angle, $\cosh(\theta) = ({\bf u}\cdot{\bf v})$; then copy the two parts of the previous result:

$$\begin{eqnarray*} \cosh(\gamma)&=& \cosh(\alpha)\cosh(\beta)+\sinh(\alpha)\si... ...+ \\ & & ( {\bf u}\times {\bf v}) \sinh(\alpha) \sinh(\beta). \end{eqnarray*}$$

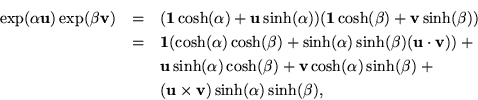
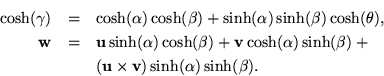
Somewhere between trivial and formidable, the definition begins by ascertaining the angle $\vert\gamma\vert$ using a formula reminiscent of the spherical law of cosines, but in actuality the variant relevant to a two-sheeted hyperboloid of revolution. Once that much is known, the vector ${\bf w}$ is defined in terms of known quantities, for which it can be said that it lies off the plane of ${\bf u}$ and ${\bf v}$ unless they lie on a line, in which case ${\bf w}$ falls on the same line giving a much more familiar law of exponents. By the antisymmetry of the cross product, when the order of the factors is reversed, ${\bf w}$ moves to the other side of the ${\bf u}-{\bf v}$ plane.