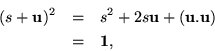
The unit quaternions are square roots of either unity or of minus one. Are there any others? According to Eq. 1, to get a root of unity needs
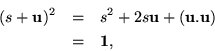
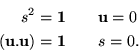
As for square roots in general, the square root of any scalar follows the same line of reasoning with the exception that everything is scaled by the positive square root of the scalar when it has one. The general requirement for
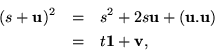
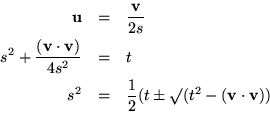
If ![]() were
were ![]() then
then ![]() would have to be zero, and only a scalar could have a vector square root. But non-vector quaternions can have quaternion roots, of which there would appear to be exactly four possible values for
would have to be zero, and only a scalar could have a vector square root. But non-vector quaternions can have quaternion roots, of which there would appear to be exactly four possible values for ![]() , not all necessarily real. For example,
, not all necessarily real. For example,
![]() .
.