eigenvalues and eigenvectors

The equations for the wave matrices would all have the form

$$\begin{eqnarray*} \left[ \begin{array}{ll} x_{i+1} \\ x_i \end{array} \righ... ...left[ \begin{array}{ll} x_i \\ x_{i-1} \end{array} \right], \end{eqnarray*}$$

whose characteristic equation, or dispersion relation, could be written in one of the other of two forms, the first favoring trigonometry and the second, half-angles:

$$\begin{eqnarray*} \mu^2 - \mu (\frac{m \lambda}{k} - 2) + 1 & = & 0, \\ (\surd\mu + \frac{1}{\surd\mu})^2 = \frac{m \lambda}{k}. \end{eqnarray*}$$

Matrices of (unnormalized) row and column eigenvectors are as before,

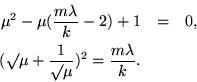
$$\begin{eqnarray*} {\rm (rows)} & = & \left[ \begin{array}{cc} \mu_+ & -1 \\ \... ...begin{array}{cc} \mu_+ & \mu_- \\ 1 & 1 \end{array} \right] \end{eqnarray*}$$

making Sylverster's theorem read:

$$\begin{eqnarray*} f(M) & = & \frac{f(\mu_+)}{(\mu_+^2 - 1)} \left[ \begin{array... ...ight] \left[ \begin{array}{cc} \mu_- & -1 \end{array} \right] \end{eqnarray*}$$