Tchebycheff polynomials

This expression simplifies drastically when 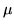$\mu$ is written as an exponential, 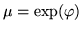$\mu = \exp(\varphi)$, and it is supposed that 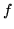$f$ is an n${}^{th}$ power:

$$\begin{eqnarray*} M^n & = & \frac{\exp(n \varphi_+)}{\exp(2\varphi_+) - 1} ... ... \exp((n+1)\varphi_-) & \exp(n\varphi_-) \end{array} \right] \end{eqnarray*}$$

Still further simplification awaits: First take exponential factors out of the denominators

$$\begin{eqnarray*} M^n & = & \frac{1}{\exp( \varphi_+) - \exp(- \varphi_+)} ... ...n \varphi_-) & - \exp((n-1) \varphi_-) \end{array} \right] \\ \end{eqnarray*}$$

and then recognize that the 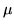$\mu$'s are reciprocals, so their logarithms are negatives. The matrix 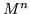$M^n$ is accordingly a function of a single angle and with common denominators the sum becomes a difference:

$$\begin{eqnarray*} M^n & = & \frac{1}{\sinh(\varphi)} \left[ \begin{array}{cc} ... ...sinh(n \varphi) & - \sinh((n-1) \varphi). \end{array} \right] \end{eqnarray*}$$

Moreover, the matrix elements, with the participation of the obstreperous denominators, are nothing other than Tchebycheff polynomialsTchebycheff polynomials of the second kind (with imaginary argument),

$$\begin{eqnarray*} U_n(\cos(\varphi)) & = & \frac{\sin((n+1)\varphi)}{\sin(\varphi)}, \end{eqnarray*}$$

the denominator 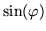$\sin(\varphi)$ generally serving to make derivatives turn out right.

$$\begin{eqnarray*} M^n & = & \left[ \begin{array}{cc} U_n(\cos(\varphi)) & - U... ...cos(\varphi)) & - U_{n-2}(\cos(\varphi)). \end{array} \right] \end{eqnarray*}$$

Some patience with trigonometric identities will confirm 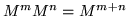$M^m M^n = M^{m+n}$, which must be so because of the context in which it occurs.

Slight additional trigonometrical transformation (writing s and c for sinh and cosh to fit the formula onto the page) produces

$$\begin{eqnarray*} M^n & = & \frac{1}{\sinh(\varphi)} \left[ \begin{array}{cc} ... ...) & -1 \\ 1 & - \cosh(\varphi) \end{array} \right] \right). \end{eqnarray*}$$

The algebra of the wave matrices having been attended to, the determination of the eigenvalues of the dynamical matrix depends on choosing appropriate boundary conditions for a relationship such as

$$\begin{eqnarray*} X_n & = & M^n X_1. \end{eqnarray*}$$