


Next: Equivalence Relations
Up: Axiomatic Viewpoint
Previous: Order relations
Contents
Pairing up elements in the style (x, f(x)) so that there is never more than one f(x) for a given x, is what defines a function f. When the sets from which x and f(x) are chosen have structure, functions preserving the structure are usually set apart from more generic functions, and often have special properties themselves. For vector spaces, requiring linearity,
does the job. However, it is easy to treat functions as though they were
vectors, by saying
so that without further ado, we can regard all of the linear functions between a fixed pair of vector spaces U and V as forming another vector space. To give
it a name, call it Linear(U,V). From such humble beginnings, all sorts of different combinations of functions and vector spaces can be constructed.
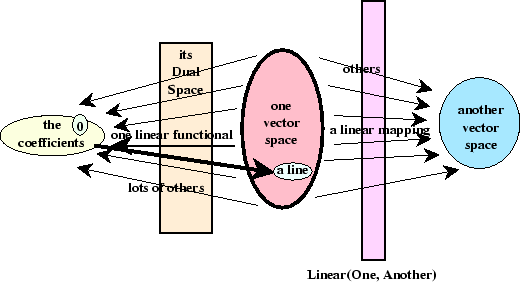
Some of the possibilities are shown in the following diagram, Figure 1.
Figure:
A schematic representation of different linear mappings.
 |
Scalar valued functions of vectors are some of the easiest functions to define, which is appropriate considering their fundamental importance. The starting point is to recall the role of a basis - every vector 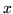 is some linear combination of basis vectors
is some linear combination of basis vectors 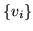 :
:
whence the value of the linear function depends entirely on the values which it assigns to the basis:
It is a great temptation to make up a whole collection of new functions, 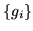 , each one charged with assigning its own basis vector the value 1, all the rest 0:
, each one charged with assigning its own basis vector the value 1, all the rest 0:
(here 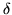 would be Kronecker's deltaKronecker delta). So doing, the function
would be Kronecker's deltaKronecker delta). So doing, the function 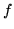 would end up being represented by
would end up being represented by
which in turn would make the 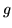 's into a basis for scalar valued functions of vectors. This new space, of the same dimension as the old, is called its dual space. It is noteworthy that the dual of a dual reverts back to the original space, thanks to the fact that arguments can map their functions into values, all in a completely linear fashion.
's into a basis for scalar valued functions of vectors. This new space, of the same dimension as the old, is called its dual space. It is noteworthy that the dual of a dual reverts back to the original space, thanks to the fact that arguments can map their functions into values, all in a completely linear fashion.
Just because a space and its dual have the same dimension, they have to be practically identical. They both have bases, but it remains to be seen just how both bases could be drawn in the same picture the way vectors are usually visualized. First, though, it is convenient to discuss functions of several vectors, and then to make up biorthogonal bases.



Next: Equivalence Relations
Up: Axiomatic Viewpoint
Previous: Order relations
Contents
Pedro Hernandez
2004-02-28
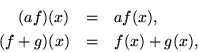
![]() is some linear combination of basis vectors
is some linear combination of basis vectors ![]() :
: