


Next: Point defect
Up: A Variety of String
Previous: boundary conditions and the
Contents
Solving a uniform string with wave matrices requires powers of a single wave matrix, which turns out to be a convenient combination of Tchebycheff polynomials. Mixing wave matrices for nonuniform strings is more complicated algebraically, not only because the wave matrices don't commute, but also because the wave matrix at the joint is slightly different. To start with a simple example, consider two dissimilar strings joined together.
Figure:
two strings spliced by a single connecting spring
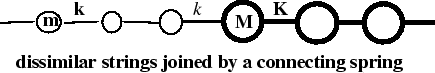 |
The dynamical matrix would look like:
with two lines of recursion differing from those in the main body of the matrix. They only affect the wave matrix in the respect that its 12 element is no longer 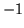 , but something else. In terms of masses
, but something else. In terms of masses 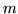 and
and 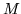 , with elastic constants
, with elastic constants 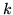 ,
, 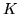 , and an intermediate
, and an intermediate 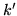 , we need
, we need
in terms of their eigenvalues and eigenvectors (or else to endure the algebra resulting from using them in their crude form).
A first observation is that the two new wave matrices are probably not unimodular (determinant 1), an essential requirement for the derivation of the uniform chain just given, but easily remedied by division of the whole matrix by the square root of their determinant. The result is
with dispersion relation
as before, it can be rewritten
the half-angle formula could even be extracted with a little initiative. However, the eigenvector matrices change over into
leaving a normalization factor of
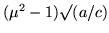 for Sylvester's theorem, which is not only a numerical multiple of the previous normalizer, but one which is the same for both eigenvalues. Moreover the projectors themselves will behave consistently, with the net result that the Tchebycheff polynomials will have some numerical factors, and the angle of their argument will be slightly different.
for Sylvester's theorem, which is not only a numerical multiple of the previous normalizer, but one which is the same for both eigenvalues. Moreover the projectors themselves will behave consistently, with the net result that the Tchebycheff polynomials will have some numerical factors, and the angle of their argument will be slightly different.
In the end it is necessary to calculate
for 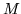 particles of one type and
particles of one type and 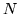 of the other.
Even before working out the details, it is not hard to foresee the results. If the element
of the other.
Even before working out the details, it is not hard to foresee the results. If the element 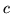 in the dynamical matrix were zero, there would be two independent chains which would follow the guidelines already worked out for uniform chains, which means two cosinusoidal spectra with sinusoidal eigenvectors, although the exact nature of their boundary conditions would have to be worked out. To first order, the perturbation
in the dynamical matrix were zero, there would be two independent chains which would follow the guidelines already worked out for uniform chains, which means two cosinusoidal spectra with sinusoidal eigenvectors, although the exact nature of their boundary conditions would have to be worked out. To first order, the perturbation 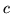 should not change the eigenvalues, but would result in a slight adjustment to the eigenvectors, in magnitude depending on the relation of eigenvalue difference to matrix elements. Mainly, the waves could no longer be zero in each other's domains, as they would have been before.
should not change the eigenvalues, but would result in a slight adjustment to the eigenvectors, in magnitude depending on the relation of eigenvalue difference to matrix elements. Mainly, the waves could no longer be zero in each other's domains, as they would have been before.
Figure:
Normal modes of a split chain of eleven particles with with fixed ends and two different masses.
 |

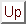


Next: Point defect
Up: A Variety of String
Previous: boundary conditions and the
Contents
Pedro Hernandez
2004-02-28
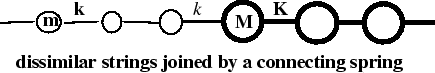
![\begin{eqnarray*}
A & = &
\left[ \begin{array}{cccccccccc}
\ldots & . & . & ...
...ts & . & . & . & . & . & . & . & . & \ldots
\end{array} \right]
\end{eqnarray*}](img471.gif)
![\begin{eqnarray*}
{\rm (rows)} & = & \left[ \begin{array}{cc}
\mu_+ & - \surd...
...{c}\mu_+ & \surd\frac{a}{c}\mu_- \\ 1 & 1
\end{array} \right]
\end{eqnarray*}](img477.gif)
