boundary conditions and the spectrum

An expedient, and sometimes physically appropriate, condition is to suppose that the string closes upon itself, treating the first particle as though it were an $(n+1)^{st}$ particle; the cyclic boundary condition would require a unit matrix:

$$\begin{eqnarray*} M^n & = & I. \end{eqnarray*}$$

Two of the four requirements on the matrix elements of $M^n$ are identical but all four are consistent:

$$\begin{eqnarray*} U_{n-1}(\cosh(\varphi)) & = & 0, \\ \frac{\sinh(n \varphi)}{\sinh(\varphi)} & = & 0, \\ \varphi & = & i\frac{k \pi}{n}. \end{eqnarray*}$$

With such values of $\varphi$ ($\varphi = 0$ being excluded), $\mu = \exp(i\frac{k \pi}{n})$, leaving

$$\begin{eqnarray*} \lambda & = & \frac{4k}{m} \cos(2\frac{k\pi}{2 n}) \end{eqnarray*}$$

Figure: the dispersion relation for a uniform string

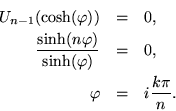
To check whether this is credible, suppose there is only one single particle. Then no shift is needed, $n = 1$, and $M$ ought to be the unit matrix. So $\lambda = 0$, there is no restoring force, and the result is correct. If there were two particles, $\lambda = 0$ persists, but for $k = 1$, $\lambda = 2k/m$ is also possible, appropriate to having a pair of springs to connect the particles.

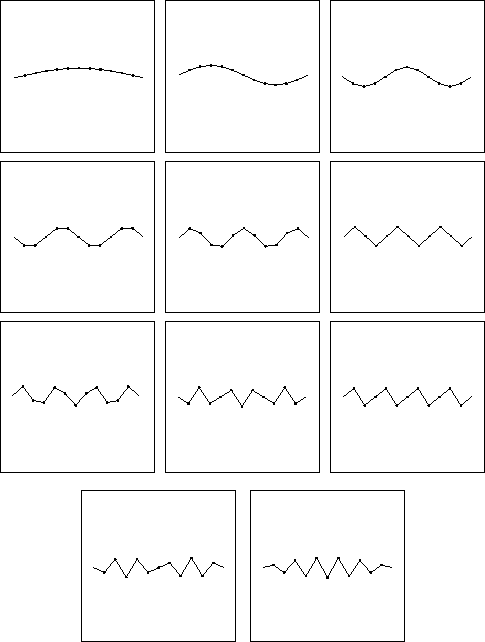
Altogether there are many other ways of assigning boundary conditions to a string. which can be broadly subclassified into boundary values and boundary conditions. A boundary value specifies the value of a component, such as making it zero to signify that the particle is constrained so that it cannot move. A boundary condition specifies a linear combination of components, and would be realized as a row vector whose inner product with a wave vector would vanish, for instance. The two kinds of condition mostly state the same information in two different ways. Whatever their form, an expression relating elements of the wave matrix must vanish, producing a polynomial equation which is the characteristic polynomial of the dynamical matrix. Since the arguments of the polynomial are built from wave numbers, the characteristic equation is a dispersion relation.

Figure: Normal modes of a uniform chain of eleven particles with with fixed ends. The amplitude distribution of the displacements of the particles is sinusoidal, each normal mode displaying one additional node as its frequency increases. The only nodes for the lowest frequency are the points of restraint, each particle having approximately the same displacement as its neighbors. Nodes for the highest frequency lie between adjacent particles, each of which keeps as great a distance from its neighbor as possible.