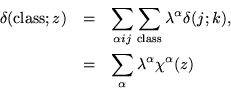Characters

The basis relations for group functions can be rearranged by taking traces of the matrix elements, and noticing that traces are invariant under change of basis. On the one hand, traces are invariants of equivalences so the result will not depend on changing to an equivalenmt representation. On the other, the same is true for internal equivalences of the group, making traces functions of classes, not merely of individual group elements. The trace is a function for which the classes are equivalence classes.

The trace-valued group function is called a charactercharacter for its representation, defined by

$$\begin{eqnarray*} \chi^\alpha(g) & = & \sum_{i=1}^{\dim(\Gamma)} d^\alpha_{ii}(g). \end{eqnarray*}$$

Especially note that $\chi^\alpha(e) = \dim(\Gamma^\alpha)$. On taking the appropriate sums in the biorthogonality relations,

$$\begin{eqnarray*} \frac{1}{\vert G\vert} \sum_{g\varepsilon G}{\chi^\alpha(g^{-1}) \chi^\beta(g)} & = & \delta(\alpha,\beta). \end{eqnarray*}$$

Because of the constancy over classes, the result is also a biorthogonality relation for class space. Call a typical class $C_i$, observe that the set of inverses of class members is another class (maybe the same one), and average within classes (where the number of elements in class $C_i is \vert C_i\vert$)to get

$$\begin{eqnarray*} \frac{1}{\vert G\vert} \sum_{C_i}\vert C_i\vert{\chi^\alpha(C_i^{-1}) \chi^\beta(C_i)} & = & \delta(\alpha,\beta). \end{eqnarray*}$$

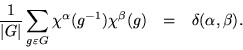
There is now a new function space, mapping classes to complex numbers, for which the characters of the irreducible representations form a biorthonormal set, which would mean that the number of inequivalent irreducible representations cannot exceed the number of classes.

As remarked, characters are not only insensitive to equivalences arising within the group, but to external influences as well. That all equivalent representations have the same character allows their characterization, which was undoubtedly the origin of the term. Beyond that, if a representation is reducible, the biorthonormality of characters permits finding out which irreducible representations are in the blocks. For a representation $\Gamma = \{D(g)\}$,

$$\begin{eqnarray*} \chi(g) & = & \sum{\chi_\alpha(g)} \\ & = & {\sum}^\prime{ n_\alpha \chi_\alpha(g)}, \end{eqnarray*}$$

the prime implying a sum over inequivalent representations and $n_\alpha$ counting the multiplicity of each irreducible representation.

$$\begin{eqnarray*} \frac{1}{\vert G\vert}\sum_G{\chi(g^{-1})\chi(g)} & = & \sum{n_\alpha^2} \end{eqnarray*}$$

For the sum to be exactly $1$ would be indicative that the representation was irreducible. As a further result, note that the trace of an element in a permutation representation is the number of fixed points for that particular element. The regular representation is a permutation representation for which only the identity fixes any points - all of them. Therefore

$$\begin{eqnarray*} \chi^{\rm regular}(g) & = & \left\{\begin{array}{ll} \vert G\vert & g = e \\ 0 & {\rm otherwise} \end{array} \right. \end{eqnarray*}$$

For whatever representation, the trace of the identity is its dimension, so $\chi^\alpha(e) = \dim(\Gamma^\alpha) = d_\alpha$; in comparison with the regular representation, for which all traces except the identity vanish, the other traces do not mattter. So

$$\begin{eqnarray*} \frac{1}{\vert G\vert}\sum_G{\chi^{\rm regular}(g^{-1})\chi^\alpha(g)} & = & d_\alpha \end{eqnarray*}$$

and each irreducible representation present is repeated its own dimensionality number of times. The important thing here is that it doesn't matter how an irreducible representation was manufactured, working with the space of complex valued group functions guarantees its place in the regular representation, and the sum of the squares of all their dimensions adds up to the order of the group.

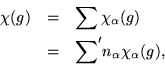
At the same time, because the regular representation contains an equivalent of any irreducible representation at all, their characters have to be present among the complex valued class functions. The only obstacle to knowing that the number of irreducible representations is equal to the number of classes would be to show that the characteristic function of a class was a linear combination of characters. Pretty much by definition, the reverse is true, characters are linear combinations of characteristic functions of classes.

We already know that the characteristic functions of points are linear combinations of matrix elements; if

$$\begin{eqnarray*} f(g) & = & \sum_{\alpha i j}{c_{\alpha i j} d^\alpha_{ij}(g)}, \end{eqnarray*}$$

taking inner products with dual basis elements gives

$$\begin{eqnarray*} (f(g),d^\alpha_{ij}(z)) & = & c^{\alpha}_{ij}, \\ f(g) & = ... ...& = & \sum_{\alpha\ i\ j}{d^\alpha_{ij}(z^{-1})d^\alpha_{ij}(g)} \end{eqnarray*}$$

The sum of products of matrix elements is either zero or one; but that was the conclusion from Schur's lemmas.

Next, consider that a class arises from finding conjugates from within the group: elements for which $x s = s y$ for all $s$. So sums over a class just average these conjugacies: $s(x+y+z+\ldots) = (x+y+z+\ldots)s$. Representationwise here is a matrix commuting with an irreducible representation, so

$$\begin{eqnarray*} \sum_{\rm class}d^\alpha_{ij}(g) & = & \lambda^{\alpha}\delta(j;k), \end{eqnarray*}$$

$\lambda^\alpha$ being the multiplier of the identity in the $\alpha^{th}$ irreducible representation.

$$\begin{eqnarray*} \delta({\rm class};z) & = & \sum_{\alpha i j}{\sum_{\rm cla... ...}}, \\ & = & \sum_{\alpha}{\lambda^{\alpha} \chi^{\alpha}(z)} \end{eqnarray*}$$

which makes the characteristic function of a class a linear combination of characters, and the characters indeed form a basis for all complex valued class functions. So we now know that the number of irreducible representations equals the number of classes, and is not just limiter by their number.