


Next: Períodos
Up: Redes
Previous: Redes
Si 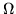 es cualquier red y
es cualquier red y
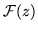 cualquier función de una
variable compleja, denotamos por :
cualquier función de una
variable compleja, denotamos por :
la sumatoria de
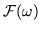 sobre los elementos
sobre los elementos
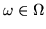 .
Y por
.
Y por
la suma sobre todos los elementos de 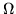 diferentes de cero,
es decir, igual a la sumatoria anterior, pero el término
diferentes de cero,
es decir, igual a la sumatoria anterior, pero el término 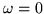 es omitido.
es omitido.
Teorema 2
Para cualquier red
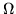
y cualquier entero
n>2,
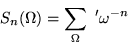 |
(1.6) |
converge absolutamente.
Si 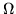 es una red doble, los puntos de la red pueden ser
distribuidos en conjuntos quedando sobre los perímetros de una
secuencia de paralelogramos concéntricos, similar a la celda unidad,
aquellos sobre el r-ésimo perímetro existen de la forma
es una red doble, los puntos de la red pueden ser
distribuidos en conjuntos quedando sobre los perímetros de una
secuencia de paralelogramos concéntricos, similar a la celda unidad,
aquellos sobre el r-ésimo perímetro existen de la forma
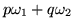 ,
donde
,
donde
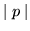 ,
,
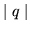 ambos
ambos 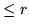 ,
y al menos uno de ellos igual a r.
,
y al menos uno de ellos igual a r.
Las cantidades
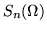 definida como en 1.6, claramente satisface la propiedad de homogeneidad:
definida como en 1.6, claramente satisface la propiedad de homogeneidad:
para todos los enteros n>2. Luego si n es impar
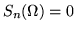 para cualquier red
para cualquier red 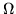 ,
ya que
,
ya que
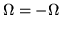 ,
entonces
,
entonces
De manera similar si 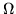 es una red cuadrada como
es una red cuadrada como
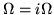 ,
cumple que
,
cumple que
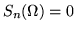 para todo n que no es divisible por 4.
para todo n que no es divisible por 4.



Next: Períodos
Up: Redes
Previous: Redes
Microcomputadoras
2001-03-09
![]() es cualquier red y
es cualquier red y
![]() cualquier función de una
variable compleja, denotamos por :
cualquier función de una
variable compleja, denotamos por :
![]() es una red doble, los puntos de la red pueden ser
distribuidos en conjuntos quedando sobre los perímetros de una
secuencia de paralelogramos concéntricos, similar a la celda unidad,
aquellos sobre el r-ésimo perímetro existen de la forma
es una red doble, los puntos de la red pueden ser
distribuidos en conjuntos quedando sobre los perímetros de una
secuencia de paralelogramos concéntricos, similar a la celda unidad,
aquellos sobre el r-ésimo perímetro existen de la forma
![]() ,
donde
,
donde
![]() ,
,
![]() ambos
ambos ![]() ,
y al menos uno de ellos igual a r.
,
y al menos uno de ellos igual a r.
![]() definida como en 1.6, claramente satisface la propiedad de homogeneidad:
definida como en 1.6, claramente satisface la propiedad de homogeneidad: