


Next: Funciones de Weierstrass
Up: Funciones Elípticas
Previous: Funciones Elípticas
Propiedades de funciones elípticas.
Si
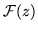 es una función elíptica, entonces las únicas
singularidades posibles de
es una función elíptica, entonces las únicas
singularidades posibles de 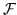 son un número finito
de polos en cada paralelogramo-periódico.
Podemos por tanto elegir un paralelogramo-periódico de tal
forma que no tenga polos sobre los lados del mismo, con
son un número finito
de polos en cada paralelogramo-periódico.
Podemos por tanto elegir un paralelogramo-periódico de tal
forma que no tenga polos sobre los lados del mismo, con
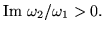
Teorema 4 (Liouville.)
Este declara que cualquier función la cual es analítica y acotada en el
plano completo es una constante.
Teorema 5
No hay funciones enteras doble periódicas
2.2.
Teorema 6
Si dos funciones elípticas tienen la misma red de periodos, las mismas
clases residuo de polos, y las mismas clases residuo de ceros, de el mismo
orden en cada caso, el cociente de las dos funciones es una constante
diferente de cero.
Teorema 7
Si dos funciones elípticas tienen la misma red de periodos, y las
mismas clases residuo de polos, con igual parte infinita en cada polo, las
funciones difieren por una constante.
Teorema 8
Sea
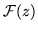
una función elíptica con la red
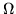
de periodos,
zeros de orden
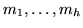
en las clases residuo
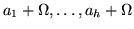
,
y polos de orden
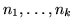
en
las clases residuo
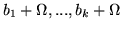
,
con residuos
r1,...,
rk respectivamente.Entonces
- i)
-
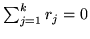
- ii)
-
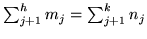
- iii)
-
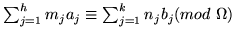
El primer punto es conocido como el teorema del residuo.
El punto ii puede ser entendido como: ``Una función elíptica
no constante tiene tantos polos como ceros''. Así que el orden de
una función elíptica puede redefinirse como el número de ceros en
un paralelogramo-periódico.
Teorema 9
La suma de los ordenes de los polos de una función doble periódica en
un paralelogramo-periódico es, al menos, 2.
De aquí podemos concluir que el orden menor de una función
elíptica es 2.
Nos parece apropiado en este momento, mencionar los dos tipos más
simples de funciones elípticas:
- 1.
- Funciones con un único polo de orden 2, en el cual la parte
principal es de la forma
en cada paralelogramo-periódico. Un ejemplo de estas funciones es
la 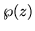 de Weierstrass.
de Weierstrass.
- 2.
- Funciones con dos polos simples cuya parte principal esta conformada por
en cada paralelogramo-periódico. Las funciones de Jacobi sn(u),
cn(u), dn(u) son un ejemplo de éstas.
Teorema 10
Si
aj y
bj son los ceros y los polos de una función de doble periodo
en un paralelogramo-periódico, entonces
donde
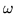
es periodo, y donde cada
aj y
bj son contados de acuerdo a su multiplicidad.



Next: Funciones de Weierstrass
Up: Funciones Elípticas
Previous: Funciones Elípticas
Microcomputadoras
2001-03-09
![]() es una función elíptica, entonces las únicas
singularidades posibles de
es una función elíptica, entonces las únicas
singularidades posibles de ![]() son un número finito
de polos en cada paralelogramo-periódico.
Podemos por tanto elegir un paralelogramo-periódico de tal
forma que no tenga polos sobre los lados del mismo, con
son un número finito
de polos en cada paralelogramo-periódico.
Podemos por tanto elegir un paralelogramo-periódico de tal
forma que no tenga polos sobre los lados del mismo, con
![]()