Funciones de Weierstrass

Se denota un par de generadores para una red de periodos, de una función elíptica por $2\omega_1, 2\omega_2$; y denotamos la misma red por $2\Omega$, donde $\Omega$ es generada por $\omega_1$ y $\omega_2$. Si deseamos especificar la red de periodos con la que la función elíptica ${\cal F} (z)$ ha sido construida la escribiremos como ${\cal F} (z\mid 2\Omega)$,

Definimos para cualquier entero $n\geq 3$

$$P_n(z\mid 2\Omega) = \sum_\Omega (z - 2\omega)^{-n}$$

Esta serie converge absoluta y uniformemente en cualquier región finita, la cual excluye de manera finita a todos los puntos de la red, tal que $\vert z\vert < K,\;\; \vert z-2\omega\vert>k$ donde $K,\; k$ son constantes positivas.

Para todo z en la región, y para todo $\omega$ tal que

$$\vert\omega\vert\;>\; K \hspace{.2in} \mbox{y} \hspace{.2in} \vert z-2\omega\vert\;>\;\vert\omega\vert,$$

así la serie está acotada superiormente por $S_n(\Omega)$.

Tomando K suficientemente grande y k suficentemente pequeño, se puede hacer que la región de convergencia incluya cualquier punto del plano, excepto puntos de la red de la forma $z = 2\omega$; por lo que P_n(z) es analítica excepto en los puntos de la red. Estos son polos de orden n con parte infinita $(z-2\omega)^{-n}$. Ya que si omitimos el término $(z-2\omega)^{-n}$ de la serie, el punto $z = 2\omega$ puede incluirse en la región de convergencia.

Si $\omega_0$ es cualquier elemento de $\Omega$, $2\omega_0$ es un periodo de P_n(z), ya que la substitución de $z+2\omega_0$ por z sólo permuta los términos de la serie ya que los conjuntos $\Omega, \Omega-\omega_0$ son los mismos (y la convergencia es absoluta) por lo que la suma no se altera.

Así $P_n(z\vert 2\Omega)$ es una FUNCION ELIPTICA DE ORDEN N, con red de periodos $2\Omega$. Además diferenciando la serie término por término, tenemos:

P'_n(z) = -nP_n+1 (z).

Sin embargo, para n=2 la serie correspondiente no converge, como debería esperarse al definir $S_2(2\Omega)$, la cual no converge. Para obtener una función elíptica de orden 2 en esta secuencia definimos:

$$\wp(z)=\wp(z\mid 2\Omega)= z^{-2}+\sum_\Omega\ '\{(z-2\omega)^{-2}-(2\omega)^{-2}\}$$

Esta serie converge absoluta y uniformemente en el mismo tipo de región ( $\vert z\vert<K,\; \vert z-2\omega\vert>k$ para todo $\omega\in\Omega$) como en las series definidas para P_n(z) con $n\geq 3$.

Diferenciando la serie término por término obtenemos

$$\wp'(z) = -2z^{-3}+\sum_\Omega\ '\left\{\frac{2}{(z-2\omega)^3} \right\} = -2P_3(z)$$

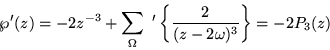
De estas series, las ecuaciones

$$\begin{eqnarray*}\wp' (z+2\omega_1) & = & \wp' (z) \\ \wp' (z+2\omega_2) & = & \wp' (z) \end{eqnarray*}$$

se sigue inmediatamente; que $\wp '(z)$ es una función elíptica.

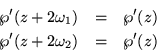
Nuevamente, integrando obtenemos

$$\wp(z+2\omega) = \wp(z) + C,$$

Ahora sea $z = -\omega$; entonces

$$\wp(\omega) = \wp(-\omega) + C = \wp(\omega) + C,$$

luego C=0. Así

$$\wp(z+2\omega) = \wp(z)$$

En consecuencia, $\wp (z)$ es una función elíptica de orden 2 con red de periodos $2\Omega$ y polos dobles en la clase residuo cero.

Corolario 1   Si n es cualquier entero, $\wp(z)^n$ es una función elíptica.

Teorema 11   La derivada de una función elíptica es una función elíptica.