


Next: Análisis de una función.
Up: Funciones de Weierstrass
Previous: Homogeneidad de y
Sea 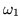 real y
real y 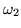 imaginario puro.
imaginario puro. 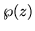 es real
sobre todos los lados de los rectángulos formando la red
es real
sobre todos los lados de los rectángulos formando la red 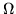 de medios-periodos. Como z describe continuamente el perímetro
de cualquier rectángulo, de z=0 a
de medios-periodos. Como z describe continuamente el perímetro
de cualquier rectángulo, de z=0 a
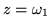 ,
luego para
,
luego para
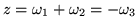 ,
después para
,
después para
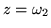 ,
y
finalmente regresando a z=0, la
,
y
finalmente regresando a z=0, la 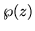 varía continuamente a
través de valores reales exclusivamente, desde
varía continuamente a
través de valores reales exclusivamente, desde 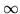 hasta
hasta 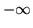 ;
por lo tanto debe asumir cada valor real sólo una vez en el curso de la
variación. Ya que la trayectoria no contiene dos valores distintos de z;
z' satisface que
;
por lo tanto debe asumir cada valor real sólo una vez en el curso de la
variación. Ya que la trayectoria no contiene dos valores distintos de z;
z' satisface que
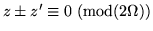 .
Por lo tanto la
variación es un decremento uniforme de
.
Por lo tanto la
variación es un decremento uniforme de 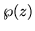 a través de valores
reales. Conforme z varia en el perímetro a través de los valores
a través de valores
reales. Conforme z varia en el perímetro a través de los valores
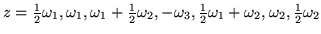 tenemos
e1 + d1 > e1 > e2 - d2 > e3 > e1 - d1 > e2 > e2 + d2,
todos estos valores son reales (como
tenemos
e1 + d1 > e1 > e2 - d2 > e3 > e1 - d1 > e2 > e2 + d2,
todos estos valores son reales (como
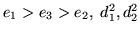 ambos
son positivos, las raíces cuadradas de d1, d2, como están
definidas, son positiva y negativa respectivamente; d32 a su vez es
negativa, así que la
ambos
son positivos, las raíces cuadradas de d1, d2, como están
definidas, son positiva y negativa respectivamente; d32 a su vez es
negativa, así que la
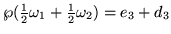 ,
,
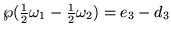 son
imaginarios conjugados).
son
imaginarios conjugados).
Además un resultado curioso es que si Re(z) es la mitad de un
múltiplo impar de 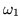 ,
,
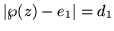 ;
si
;
si
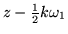 es un imaginario puro y k es un entero
impar, entonces la
es un imaginario puro y k es un entero
impar, entonces la
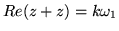 ,
es decir
,
es decir
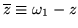 (mod (
(mod (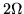 )) y
)) y
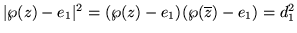 .
Similarmente
.
Similarmente
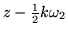 es real, donde nuevamente k es
un entero impar,
es real, donde nuevamente k es
un entero impar,
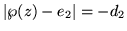 ,
ya que
,
ya que
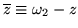 (mod (
(mod (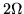 )).
)).
Las regiones de valores reales de la 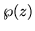 en el plano Z son las
líneas horizontales y verticales a través de todos los puntos de la
red
en el plano Z son las
líneas horizontales y verticales a través de todos los puntos de la
red 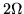 ,
y también las líneas horizontales y verticales que
están en medio de éstas. Sobre las primeras horizontales los
valores de
,
y también las líneas horizontales y verticales que
están en medio de éstas. Sobre las primeras horizontales los
valores de 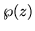 oscilan entre
oscilan entre 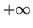 y el mínimo e1, y
sobre las otras horizontales oscilan entren
y el mínimo e1, y
sobre las otras horizontales oscilan entren 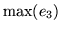 y el
y el 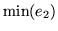 ;
sobre las primeras líneas verticales oscilan entre
;
sobre las primeras líneas verticales oscilan entre 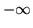 y el
y el
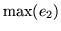 y sobre las otras verticales entre el
y sobre las otras verticales entre el 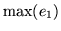 y el
y el
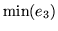 .
Note que cada valor estacionario es un valor máximo
real sobre la línea horizontal o vertical que pasa por el punto
estacionario, y un mínimo sobre el otro.
.
Note que cada valor estacionario es un valor máximo
real sobre la línea horizontal o vertical que pasa por el punto
estacionario, y un mínimo sobre el otro.



Next: Análisis de una función.
Up: Funciones de Weierstrass
Previous: Homogeneidad de y
Microcomputadoras
2001-03-09
![]() ,
,
![]() ;
si
;
si
![]() es un imaginario puro y k es un entero
impar, entonces la
es un imaginario puro y k es un entero
impar, entonces la
![]() ,
es decir
,
es decir
![]() (mod (
(mod (![]() )) y
)) y
![]() .
Similarmente
.
Similarmente
![]() es real, donde nuevamente k es
un entero impar,
es real, donde nuevamente k es
un entero impar,
![]() ,
ya que
,
ya que
![]() (mod (
(mod (![]() )).
)).
![]() en el plano Z son las
líneas horizontales y verticales a través de todos los puntos de la
red
en el plano Z son las
líneas horizontales y verticales a través de todos los puntos de la
red ![]() ,
y también las líneas horizontales y verticales que
están en medio de éstas. Sobre las primeras horizontales los
valores de
,
y también las líneas horizontales y verticales que
están en medio de éstas. Sobre las primeras horizontales los
valores de ![]() oscilan entre
oscilan entre ![]() y el mínimo e1, y
sobre las otras horizontales oscilan entren
y el mínimo e1, y
sobre las otras horizontales oscilan entren ![]() y el
y el ![]() ;
sobre las primeras líneas verticales oscilan entre
;
sobre las primeras líneas verticales oscilan entre ![]() y el
y el
![]() y sobre las otras verticales entre el
y sobre las otras verticales entre el ![]() y el
y el
![]() .
Note que cada valor estacionario es un valor máximo
real sobre la línea horizontal o vertical que pasa por el punto
estacionario, y un mínimo sobre el otro.
.
Note que cada valor estacionario es un valor máximo
real sobre la línea horizontal o vertical que pasa por el punto
estacionario, y un mínimo sobre el otro.