

Next: Períodos de la función
Up: Análisis de una función.
Previous: Análisis de una función.
La función que se propone analizar es la siguiente:
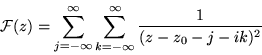 |
(3.1) |
Donde 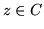 ,
z0 es una constante compleja, y los índices
,
z0 es una constante compleja, y los índices
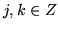 forman el número complejo
w = j + ik. Es fácil ver
que
forman el número complejo
w = j + ik. Es fácil ver
que
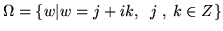 es una red
doble en el plano complejo con generadores (1,0) y (0,1).
La constante z0 indica un corrimiento de la gráfica, así que
originalmente consideramos z0 = 0, con lo que la ecuación 3.1
queda de la siguiente forma:
es una red
doble en el plano complejo con generadores (1,0) y (0,1).
La constante z0 indica un corrimiento de la gráfica, así que
originalmente consideramos z0 = 0, con lo que la ecuación 3.1
queda de la siguiente forma:
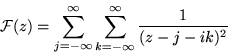 |
(3.2) |
Y sus representaciones gráficas del valor absoluto de la función son
las figuras 3.1, 3.2 y 3.3 para la superficie, contorno
de nivel y contorno de fase, respectivamente.
Figure 3.2:
Contorno de nivel
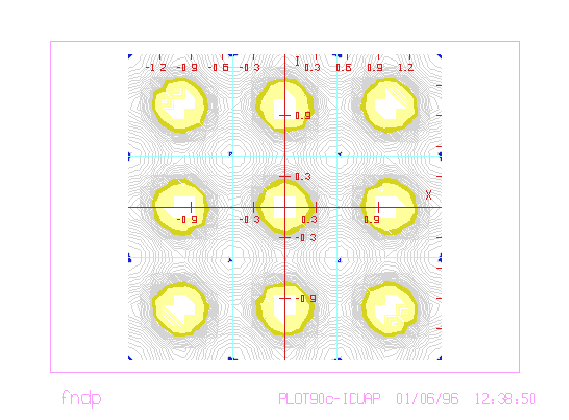 |
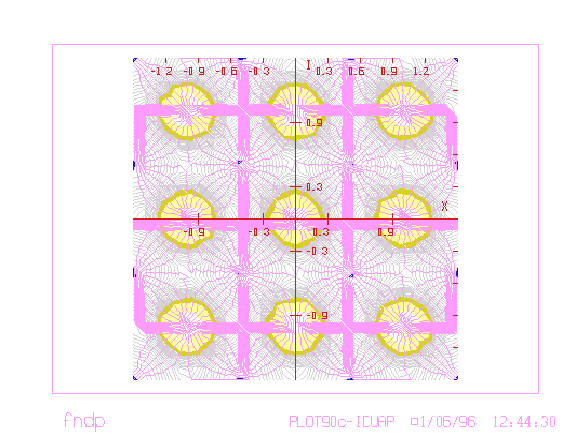
Figure 3.3:
Contorno de fase
 |



Next: Períodos de la función
Up: Análisis de una función.
Previous: Análisis de una función.
Microcomputadoras
2001-03-09