



Next: Möbius transformations representable as
Up: Functions of a complex
Previous: one-to-one and invertible
One of the things which can be done with the Möbius transformation
| d w z + c w + b z + a |
= |
0 |
(21) |
is to find relationships amongst the variables which do not depend on the coefficients of the transformation. One procedure is to try it out for four points, which is the number of coefficients, to get simultaneous equations.
| d w1 z1 + c w1 + b z1 + a |
= |
0 |
(22) |
| d w2 z2 + c w2 + b z2 + a |
= |
0 |
(23) |
| d w3 z3 + c w3 + b z3 + a |
= |
0 |
(24) |
| d w4 z4 + c w4 + b z4 + a |
= |
0 |
(25) |
The corresponding matrix equation,
can only hold when the determinant of the square matrix vanishes. That relationship invites a series of transformations which can ultimately produce the result
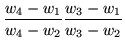 |
= |
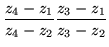 |
(26) |
This quantity equates the cross ratioscross ratio of the two sets of numbers,
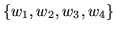 and
and
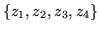 ,
it being that the cross ratio is an invariant of the Möbius transformation.
,
it being that the cross ratio is an invariant of the Möbius transformation.
The equivalence of this result to the vanishing determinant is not immediately obvious, although it can be verified by careful attention to algebraic rearrangement. A line of reasoning which suggests a result which then can subsequently be confirmed begins with the fractional linear form of the Möbius transformation,
| w |
= |
 |
(27) |
which clearly maps z1 to zero and z3 to infinity, as long as they are distinct. As for counterimages, zero maps into z1/z3, and infinity to unity. However, this is not the only formula which could map those pairs of points; any multiple of the function will do the same; a third pair of points could be introduced to resolve the ambiguity. A convenient set of points is
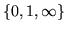 ,
which suggests selecting a point z2 to map into unity and removing the ambiguity. Thus consider
,
which suggests selecting a point z2 to map into unity and removing the ambiguity. Thus consider
| w |
= |
 |
(28) |
which is one of the cross ratios in the invariant expression Eq 26. In fact, by setting up matching expressions in w and z, any three distinct points
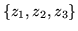 can be mapped into any other three distinct points
can be mapped into any other three distinct points
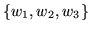 by going through the virtual intermediary of
by going through the virtual intermediary of
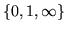 .
.




Next: Möbius transformations representable as
Up: Functions of a complex
Previous: one-to-one and invertible
Microcomputadoras
2001-04-05
![\begin{displaymath}\left[ \begin{array}{cccc}
w_1 z_1 & w_1 & z_1 & 1 \\
w_2...
...
\left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array} \right] \end{displaymath}](img44.gif)
![\begin{displaymath}\left[ \begin{array}{cccc}
w_1 z_1 & w_1 & z_1 & 1 \\
w_2...
...
\left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array} \right] \end{displaymath}](img44.gif)