To check that the derivative is well-defined, separate the complex function
into the sum of two real functions, just as z can be written as the sum of a real and an imaginary part:
| z | = | x + i y | (42) |
| f | = | u(x,y) + i v(x,y). | (43) |
By first taking ![]() real,
real,
| = | 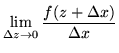 |
(44) | |
| = | 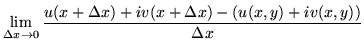 |
(45) | |
| = |  |
(46) |
| = | 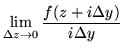 |
(47) | |
| = | 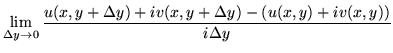 |
(48) | |
| = | 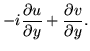 |
(49) |
Supposing that the derivative is independent of phase, at least in the context taken here, comparison shows
| = | (50) | ||
| = | (51) |
Consider the Jacobian matrix for the real functions u(x,y) and v(x,y) of the real variables x and y,
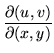 |
= | ![$\displaystyle \left[ \begin{array}{cc}
\frac{\partial u}{\partial x} & \frac{\p...
...rac{\partial u}{\partial y} & \frac{\partial v}{\partial y}
\end{array} \right]$](img90.gif) |
(52) |
| = | ![$\displaystyle \left[ \begin{array}{cc}
\frac{\partial u}{\partial x} & \frac{\p...
...rac{\partial v}{\partial x} & \frac{\partial u}{\partial y}
\end{array} \right]$](img91.gif) |
(53) | |
| = | 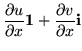 |
(54) |
The impact of the Cauchy-Riemann equations is to give the Jacobian matrix the form of a complex number in quaternion disguise; none other will suffice. Writing the matrix as an exponential shows how the derivative is a complex number with absolute value and a phase.
The conclusion is not only that not any old pair of functions could be joined to get an analytic functionanalytic function (as differentiable functions of a complex variable are called), but that by knowing one of them, one effectively knows the other. That is,
| v(x,y) - v(a,y) | = | 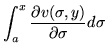 |
(55) |
| = |  |
(56) |
Knowing u, take its derivative and integrate to get v. For example, according to Euler's formula,
| ez | = | (57) |
| u | = | (58) | |
| = | (59) | ||
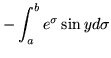 |
= | (60) | |
| v(x,y) - v(a,y) | = | (61) |
| v(x,y) | = | (62) |
So trying to think of something like
![]() as an analytic function just wouldn't work.
as an analytic function just wouldn't work.
The reason there aren't analytic quaternion functions is twofold. First, they anticommute (complicating division by ![]() ), and besides, there is getting their Jacobian matrices to act like numbers.
), and besides, there is getting their Jacobian matrices to act like numbers.
Consider anticommutativity and the derivative of q2. Having written
| = | (63) |
Historically, some progress has been made by requiring quaternion functions to satisfy linear partial differential equations similar to the Cauchy-Riemann equations. However, examining the possibilities in more detail would be a distraction from our concern with complex functions,
Remaining with functions of a complex numbers, it seems that all the manipulations which work for real variables seem to work for complex variables. That is because they are confined to polynomials and perhaps their limits, where there is always a term free of ![]() along with others having
along with others having ![]() as a factor which can vanish in the limit.
as a factor which can vanish in the limit.
But those are not the only functions of two real variables which can take complex values. Consider the complex conjugate,
| = | x - i y. | (64) |
| J(x,y) | = | ![$\displaystyle \left[ \begin{array}{cc}
1 & 0 \\ 0 & -1
\end{array} \right],$](img108.gif) |
(65) |
| = | x2 + y 2, | (66) |
| J(x,y) | = | ![$\displaystyle \left[ \begin{array}{cc}
2x & 0 \\ 2y & 0
\end{array} \right].$](img110.gif) |
(67) |