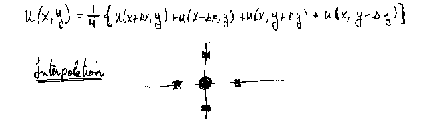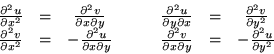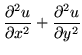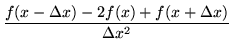Next: the Schwartz derivative
Up: The derivative of a
Previous: Cauchy-Riemann equations
Figure 8:
A harmonic function averages the values of its neighbors.
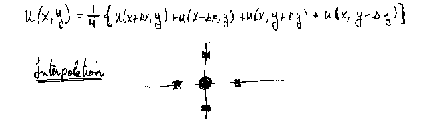 |
If an additional derivative is taken in the Cauchy - Riemann equations, we have
From the equality of mixed second partial derivatives we get
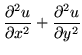 |
= |
0 |
(68) |
 |
= |
0 |
(69) |
which means that u and v satisfy the two dimensional Laplace equation and are harmonic. An important practical consequence is that such functions never have maxima nor minima (unless they are confined by a boundary). This is most easily seen by writing the second derivatives in finite difference form
 |
= |
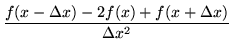 |
(70) |
so that
| u(x,y) |
= |
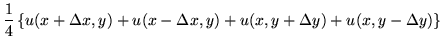 |
(71) |
| v(x,y) |
= |
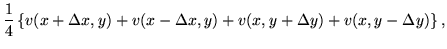 |
(72) |
or, in other words, each central value is the average of its neighbors. No average can exceed all the values it is averaging, nor fall below all of them, either. This observation is a precursor of the maximum modulus principle, which holds that the critical points of an analytic function are saddle points, and that extreme values of such a function can only occur on the boundary of a region over which it is examined.




Next: the Schwartz derivative
Up: The derivative of a
Previous: Cauchy-Riemann equations
Microcomputadoras
2001-04-05