To begin with, the usual calculus definition of a derivative can be applied to complex functions just as well as to real functions. It is just that the norm
![]() of an increment must be sent to zero, rather than the absolute value of a real difference,
of an increment must be sent to zero, rather than the absolute value of a real difference,
![]() .
.
 |
= | 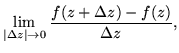 |
(38) |
From this, the usual rules governing the derivatives of sums, products, differences and quotients can be deduced. Derivatives of powers can be obtained from the binomial theorem
| = | 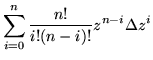 |
(39) |
| = | n zn-1. | (40) |
The chain rule for composite functions is applicable, so that the derivatives of inverse functions can be obtained. About all that remains from introductory calculus courses is to obtain the derivative of an exponential and of the trigonometric functions. At least for the exponenial, the derivative of products and the definition holding that
| ez | = | (41) |
There is one detail which can easily be overlooked in applying the limit in the definition of the derivative, which is that the result not depend on the phase of ![]() ,
just as in the real case, there would be a difference in left hand or right hand limits which could cause an ambiguity defeating the definition.
,
just as in the real case, there would be a difference in left hand or right hand limits which could cause an ambiguity defeating the definition.