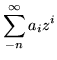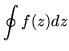evaluation of integrals by using the residues at poles

The way to deal with singularities inside a contour is to wrap the contour around them so as not to include the singularities and then cancel parts of the contour which overlap and run in opposite directions. For example, consider a singularity at the origin and surround it with two circles, one large and the other small. By breaking the circles and connecting them by two close radii, an overall singularity-free contour can be created.

By taking very close radii, their integrals can be made to cancel, leaving he difference (because of running in opposite directions whilst counting counterclockwise contours as positive) of integrals over the circles. The outer circle can be almost anything else unless it is considered to surround infinity, whereas the circular form of the inner circle is important. Surrounding its singularfity symmetrically, it can be approximated by transferring to polar coordinates, whereupon it becomes

$$i \int_\varepsilon^{2\pi-\varepsilon} r f(z) e^{i\phi} d \phi.$$

Here it is a question of what the singularity is like. If f(z) behaves like a power, or a sum of powers, we get terms like

$$i \int_0^{2\pi} r (re^{i\phi})^n e^{i\phi} d \phi i r^{n+1} \int_0^{2\pi} e^{i(n+1)\phi} d\phi$$ = (142)

which is an integral of functions averaging to zero unless n = -1. For that term, the integral turns into 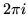$2\pi i$. Therefore isolated power-like singularities don't change the value of a contour integral enclosing them (just the power -1). Square roots and such things are another matter; the difference of the integrals along the radial arcs also has to be taken into account.

The residueresidue of a function f(z) at a point of singularity z₀ is defined by

$$\lim_{z\rightarrow z_0} (z-z_0)f(z-z_0),$$ r = (143)

which looks very much like the definition of a derivative. However, since z₀ is a point of singularity, there is no derivative there, and besides, the factor (z-z₀) sits in the numerator, where its role is to cancel out a similar divisor in the makeup of the singularity rather than in the denominator where the definition of a derivative would place it.

If f(z) had a power series expansion beginning with negative powers (a Laurent series) the residue would be the coefficient a_-1 in that series. Therefore suppose

$$\sum_{-n}^\infty a_i z^i$$ f(z) = 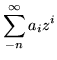(144)

which implies that an integral around a contour enclosing some or all of its singularities would be

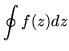$$\oint f(z) dz 2\pi i\sum_{\rm interior\ poles} r_j.$$ = (145)

The use of the residues of a complex function gives a way to evaluate many definite integrals, including what seem to be real integrals. The way to get a real definite integral is to close the half-plane above the real axis with a huge semicircle, and hope that the function vanishes sufficently rapidly as one rises in the plane. The integral over the semicircle then approaches zero as a limit as its radius increases, leaving the poles in the upper half plane to contribute their residues. There exist extensive integral tables which have been constructed in this way.