| = | (125) | ||
| = | (126) |
The basic differential relations for complex variables are the Cauchy - Riemann equations. For a function
f(z) = u(x,y) + i v(x,y) of the complex variable
z = x + i y,
| = | (125) | ||
| = | (126) |
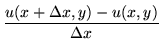 |
= | 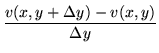 |
(127) |
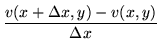 |
= | 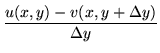 |
(128) |
Suppose that f has been defined along the real axis and that we want to know about its behavior in the upper half plane, y>0. Then
| = | 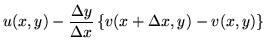 |
(129) |
Meanwhile v is changing according to
| = | 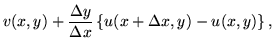 |
(130) |
Taken together, these two equations tell how to work up the positive y-axis strip by strip. Somehow that says that an analytic function is defined everywhere else by knowing its two halves on the real axis. Actually some kind of line drawn anywhere else ought to work, but this approach avoids worrying about corners and the like.
This is a kind of initial value problem, where both u and v are specified and are leapfrogged to get values somewhere else. But numerical values could be given for u and symbolic values for v. In the next strip, the v's would get numerical increments, the u's symbolic increments, but of first degree in v. Repeating, first degree expressions keep recurring until at last, in some final strip some exact values could be proposed. Then some linear equations woud have to be solved to find out what the values of the v's should have been to get the required values. The matrix just has +1's or -1's because of the sums and differences, and has to be raised to a power to get the number of parallel lines used in climbing.
Rather than flipping between u's and v's, the fact that each is harmonic can be used to work up the ladder of strips using averages. Then a row depends on two predecessors, so initial values and derivatives could be used (derivatives of u's gotten from values of v by using one of the Cauchy - Riemann equations). Also, instead of strips, think of any area, such as a rectangle. Points outside the rectangle aren't part of the differential equation but define averages, so one could try to accomodate the interior to a prescribed boundary.
Reasoning with finite differences means getting the matrices in detail and getting a good symbolic description. Usually ordinary calculus is applied to finding values at one place in terms of another.
First, line integrals.
In real analysis, an integral (at least a Riemann integral) is defined
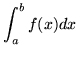 |
= | 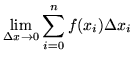 |
(131) |
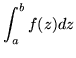 |
= | 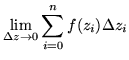 |
(132) |
The dependence can be checked out beginning with a
![]() rectangle. From the definition, we need
rectangle. From the definition, we need
| = | (133) | ||
| = | (134) |
With ![]() decomposed into its real and imaginary increments, consider the alternative orders in which they can be taken. In keeping with the spirit of Riemann integration, the function should be evaluated at the beginning of each interval of subdivision and not be allowed to retain the same value from one step to the next.
decomposed into its real and imaginary increments, consider the alternative orders in which they can be taken. In keeping with the spirit of Riemann integration, the function should be evaluated at the beginning of each interval of subdivision and not be allowed to retain the same value from one step to the next.
Using ![]() ,
then
,
then ![]() we get
we get
| = | 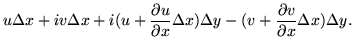 |
(135) |
| = | 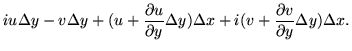 |
(136) |
It is now a matter of comparing
| (137) | |||
| (138) |
In general, the contour can be shifted across any rectangle for which a linear approximation to the function is valid, which would exclude any singularities or branch points - points where the function is not invertible and so making its definition suspect.
A consequence of path-shifting is that when the endpoint matches the initial point, the value of the integral is truly zero. Again the requirement is that the contour never has to cross over a singularity.
A useful side effect of the way Riemann integrals are defined is that the function can be defined in different ways in different places - just so long as the definitions overlap sufficiently that the Cauchy - Riemann equations hold for both definitions.
A common source of multiple definitions is to have two different Taylor's series with finite radii of convergence, centered on different points; the definitions can be compared where their disks of convergence overlap.
The vanishing of a closed contour integral is usually verified by using Green's formula, which is a useful technique in its own right. Note that the harmonicity condition makes the average over an area vanish, so that a double integral over a plane region should be zero except for boundary values which are not compensated in the sum.
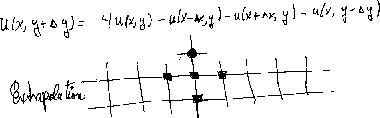 |
So add a rim to any region and fill it with values to get the zero average. To make this work, the sum over the interior - an area integral - must be the negative of the sum of the boundary values - a contour integral. In the form needed for complex variable theory, suppose that u(x,y) and v(x,y) are two real valued functions such as the real and imaginary parts of an analytic function. Further suppose that it is desired to calculate
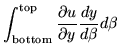 |
= | (139) | |
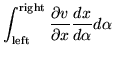 |
= | (140) |
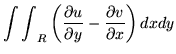 |
= |  |
(141) |
Then, by using the Cauchy - Riemann equations in the area integral to make it vanish, the vanishing of the contour integral follows.