Another application is to deliberately introduce a singularity and then to evaluate the new integral. Consider
This is Cauchy's integral representationCauchy's integral of an analytic function, which is nothing more than an integral version of the observation that an analytic function averages its surrounding values. Here each value is given the weight
![]() .
If z-z0 is written in polar form, the weight is a combination of the reciprocal of the distance of an element of arc and its angular aperture. That normalizes all arcs to an equivalent distance (that's the factor r), and performs the average.
.
If z-z0 is written in polar form, the weight is a combination of the reciprocal of the distance of an element of arc and its angular aperture. That normalizes all arcs to an equivalent distance (that's the factor r), and performs the average.
Exploiting the fact that the derivative of an integral is the integral of the derivative of its integrand,

For convenience of reference, we could just collect the formulas for the first few derivatives:
| f(z0) | = | 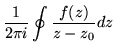 |
(146) |
| f'(z0) | = | 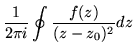 |
(147) |
| f''(z0) | = |  |
(148) |
| f(n)(z0) | = | 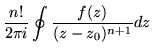 |
(149) |
Still another useful induced singularity makes use of the logarithmic derivative, supposing that there is a region containing only a finite number of zeroes and poles of f(z). Then.
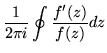 |
= | (150) |
This result, being true for any polynomial with complex coefficients, lays to rest the question of whether anything new can be gotten from taking the square root of -i (bearing in mind the humble origin of i itself). Neither x2+i nor any other combination of powers and complex numbers needs anything beside complex numbers as roots. An interesting point here is the way that the contour integral transforms the result that a power has n roots into the fact that any polynomial of that degree also has roots, although they are not necessarily (real multiples of) roots of unity.