| f(z-z0) | = | (189) | |
| = | 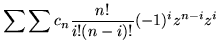 |
(190) |
Although Taylor's series have radii of convergence, the circle in which they are defined can sometimes be shifted, which means that sometimes it is possible to work one's way around singularities. One way is to write
z-z0 = (z-z1) + (z1-z0), which is best seen by turning a Maclaurin series into a Taylor's series. If
| f(z-z0) | = | (189) | |
| = | 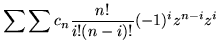 |
(190) |
![\begin{displaymath}\left[ \begin{array}{c}
1 \\ z-z_0 \\ (z-z_0)^2 \\ \ldots \e...
... \begin{array}{c} 1 \\ z \\ z^2 \\ \ldots \end{array} \right]
\end{displaymath}](img301.gif)
The expectation is that shifting and reexpansion can be used to circumvent a singularity. It should not be thought that bypassing a singularity by two routes should always give the same result; but two routes which don't surround a singularity must. This is the monodromy theoremmonodromy theorem; the process is called analytic continuationanalytic continuation.
Sometimes an attempt at continuation will strike a barrier, no matter what route is taken. That would lead to a region densely bounded by singularities.
If all the coefficients of a Taylor's series vanish at a point of analyticity, and the radius of its disk of convergence is non-zero, then the function not only vanishes throughout that disk, but everywhere else that can be reached by analytic continuation. Conversely, if a function vanishes on any convenient point set large enough to take derivatives, or to apply Cauchy's integral formula, or to perform a continuation, the Taylor's series, must be zero.
By taking differences, two functions which coincide in a similar fashion must turn out to be identical.
One way of making a continuation that sometimes works is to observe that
![]() is an analytic function whenever f is, in spite of the complex conjugations. The two conjugates cancel one another, so to speak. In terms of a Taylor's series, it is a new function of the same variable z, whose coefficients are the complex conjugates of those of the old function.
is an analytic function whenever f is, in spite of the complex conjugations. The two conjugates cancel one another, so to speak. In terms of a Taylor's series, it is a new function of the same variable z, whose coefficients are the complex conjugates of those of the old function.
Then, if a region straddles the real axis, and the function is real for real arguments, we have two functions with an arc of common values. Thus values from the upper half plane can be reflected into the lower half plane and taken as an analytic continuation of the original function.