| f(z0) | = | 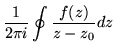 |
(182) |
Evidently polynomials and rational fractions - quotients of polynomials - are analytic functions, moreover defined in the whole complex plane if ``infinity'' is accepted as a number. There is not much trouble in extending a polynomial to an infinite series provided that its convergence is checked; a power series can be expected to have a radius of convergence. In fact, we have used he complex exponential from the beginning to get such things as Euler's formula or the solution of systems of differential equations with constant coefficients.
But the concept of a function is quite general, since the only thing required is a certain kind of set of pairs of values. That creates the problem of representing the function in a manageable form, which a table of numbers is not. Some help is given by the Cauchy integral formula,
| f(z0) | = | 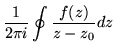 |
(182) |
| f(z1) | = | 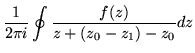 |
(183) |
| = | 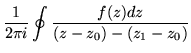 |
(184) | |
| = | 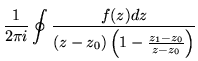 |
(185) | |
| = | 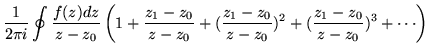 |
(186) | |
| = | 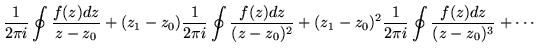 |
(187) | |
| = | 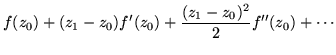 |
(188) |
Is it safe to conclude that a function is zero if its Taylor's series has all zero coefficients? For example, the function e-1/x has derivative (1/x2)e-1/x in which the zero due to e-1/x overwhelms the pole due to 1/x2 - for positive x, that is. Consider e-1/x2 which has zero derivatives from both sides at zero. But along the imaginary axis, that fails. Such functions cannot be analytic.
But these examples depend upon a failure of analyticity, so it seems that a zero series for an analytic function really represents the zero function and nothing else.
If not all coefficients are zero, but some of the leading coefficients vanish, then there is a zero at the expansion point due to a factor (z-z0)k. Then by continuity there is a small disk surrounding z0 where the function can't be zero either. Hence the zeroes of an analytic function may be multiple, but their degree is finite unless the function is actually zero.
Stated in another form, zeroes may occur in finite clusters, which must be isolated from one another, and the function can still be analytic. This excludes analyticity at a limit point of zeroes, or at zeroes of infinite multiplicity.
The same conclusions hold when the zeroes arise from the difference of two analytic functions (Can the difference of two functions be analytic when the functions themselves are not? Consider
![]() and
and
![]() .) Therefore if the functions coincide over a set which has a limit point, they are identical in any domain including the limit point. (Can infinity be a limit point? In other words if two functions agree for integer values, are they identical: Try adding
.) Therefore if the functions coincide over a set which has a limit point, they are identical in any domain including the limit point. (Can infinity be a limit point? In other words if two functions agree for integer values, are they identical: Try adding
![]() to one of them.)
to one of them.)