the differential equation for $\wp$

Liouville's theorem can be used to infer a differential equation for functions, given that they depend on poles for their existence. Consider two devices for creating new functions of the same polaritypolarity. One is squaring, or in general raising to powers, which will only change the multiplicity of whatever zeroes or poles are present, but not their location. Division, of course, will interchange zeroes and poles. Besides that, there exists the possibility of taking derivatives, which will probably change the number and location of zeroes, but only increases the order of poles without changing their location.

In the case of $\wp$, there is a double pole at the origin, implying that $\wp'$ has a triple pole there. Consequently both the cube of the function and the square of the derivative have poles of sixth order which can be cancelled by dividing them. But zeroes in the denominator can create new poles, so they must be removed; by forming linear combinations, if that is possible. Expecting to see three zeroes in $\wp'$ corresponding to the number of its poles, the attempt could be made to match them with a linear combination of $\wp^2$, $\wp$, and 1.

The algebra involved is fairly messy, but there does exist a quotient which, lacking poles, is constant by Liouville's theorem, leading to the differential equation

 

$$\wp'(z)^2 4\wp(z)^3 - g_2\wp(z) - g_3$$ = (195)

(the use of the symbols g₂ and g₃ being traditional). There is a corresponding integral,

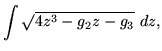$$\int \surd\overline{4z^3 - g_2z - g_3}\ dz,$$ (196)

which is related to the historical exercise of calculating the length or an arc on an ellipse. Consequently affiliated integrals are called elliptic integrals and their inverses elliptic functions.

Interestingly, because of the technique of balancing poles in quotients by which equation (195) was derived, the whole theory of elliptic functions can be based on $\wp$ and $\wp'$, notwithstanding that there are whole alternative families of variants which are more useful for some purposes or in other situations. It is probably not an exaggeration to say that the advanced mathematics of the late nineteenth century consisted in the study of elliptic functions in their manifold variations.