| = | (197) |
Although the Weierstrass function and its derivative constitute a logical
basis for the theory of elliptic functions, there is a second tradition which
is both of historical and practical importance. It can be related to the
Weierstrass form by writing the right hand side of the basic differential
equation (195) in factored form (using
traditional letters for the roots),
Given that the derivative vanishes at the roots, they are not only critical points, but good places to take square roots of what locally is nearly a square, in the expectation that the two branches will be distinguishable. Although that was not the historical reasoning, it is a good pretext to introduce the three root functions [6, §29]
| fi2(z) | = | (198) |
There is a very high symmetry inherent in these definitions; in fact the substitution of
![]() for any choice of i into equation (197) results in
for any choice of i into equation (197) results in
| (2fifi')2 | = | 4f12f22f32. | (199) |
Such a system of equations as this arises in many applications, such as the equation of motion for a heavy top about its principal axes and so was one of the historical inspirations for the study of its solutions in whatever form they took.
There is an elaborate naming system for quotients of the root functions, plus schemes for standardizing scale factors and getting convenient combinations of the roots. To this end, define
| u | = | (200) | |
| k2 | = | (201) |
| = | 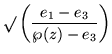 |
(202) | |
| = | 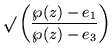 |
(203) | |
| = | 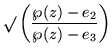 |
(204) |
Figure 14 shows a perspective view of the absolute value of the Jacobi function
![]() ,
which can be contrasted with the analogous view in Figure 13 of the Weierstrass function
,
which can be contrasted with the analogous view in Figure 13 of the Weierstrass function ![]() .
They look much the same, due to the occurrence of poles and zeroes in each unit cell. However, the Jacobi functions have two simple poles per cell whereas the Weierstrass function has just one double pole. Examination of the figures reveals many symmetries, not only the expected translational symmetry but also by reflection and combinations of translation and reflection. Beyond that, if the period lattice is square or rhombic, the functions follow suit.
.
They look much the same, due to the occurrence of poles and zeroes in each unit cell. However, the Jacobi functions have two simple poles per cell whereas the Weierstrass function has just one double pole. Examination of the figures reveals many symmetries, not only the expected translational symmetry but also by reflection and combinations of translation and reflection. Beyond that, if the period lattice is square or rhombic, the functions follow suit.
The root form (197) of the Weierstrass differential equation lends itself to calculating a Schwartz derivative. Since we already have
| = | (205) |
| = | (206) |
| = | (207) |
Another derivative,
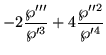 |
= | (208) |
| = | 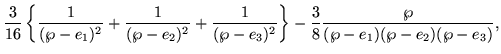 |
(209) |
This result, set forth as an exercise in Whittaker and Watson's A Course of Modern Analysis [28, chap XX, p. 439], does not seem to be used thereafter, but it invites some speculation. A periodic lattice would be expected to be invariant under affine transformations -- composites of translations with matrix products -- but Möbius transformations also include inversions, which would produce a different network entirely.
Therefore the Weierstrass equation might well not be invariant; what is interesting is that the inverse transformation is well behaved, although in the end, evaluating the Schwartz derivative is itself moderately complicated. Naturally, the Schwartz derivative of any function whatsoever can be calculated, which does not thereby automatically guarantee a useful interpretation.
In fact, the Ricatti style resolution of Schwartz derivative equations shows that the inverse Weierstrass function is a fractional linear combination of two linearly independent solutions of the second order linear differential equation
| = | 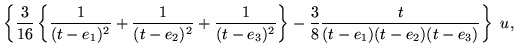 |
(210) |
This observation prompts two lines of thought. One is to repeat the derivation of the Schwartz derivative for functions which could be double valued functions of a cubic polynomial, to obtain a differential invariant for this more general class of functions. The other would be to look for automorphic functions -- those which retain their values with respect to some discrete subgroup of the unitary unimodular group of Möbius transformations. This latter alternative has been extensively studied, for example in Ford's Automorphic Functions [8].