| = | (A + B) Z | (257) | |
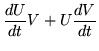 |
= | (A+B)UV | (258) |
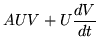 |
= | AUV + BUV | (259) |
| = | (260) |
The sum rule for exponents requires modification for matrizants, due as usual to problems of noncommutativity. Suppose that the coefficient matrix M is the sum of two others, A and B, and that it is desired to solve he system
dZ/dt = (A+B)Z. Suppose furthermore that Z is factored into Z=UV,
and that the equation dU/dt=AU has already been solved subject to the initial condition U(0)=I. Then we have, in succession,
| = | (A + B) Z | (257) | |
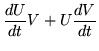 |
= | (A+B)UV | (258) |
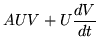 |
= | AUV + BUV | (259) |
| = | (260) |
| = | (261) | ||
| B* | = | (262) |
There is no requirement that the solution matrix be a product of solutions to linear equations, even though the overall equation is linear. Suppose that Z=PQ for some inveertible P and Q, but that the equation is still
dZ/dt = MZ. Then
The WKB method uses this transformation to diagonalize the coefficient matrix M, and then treat the new term which is introduced as a correction to which the procedure for a sum of exponents can be applied. Actually there are two parts to the WKB method, of which the more delicate is the treatment of the singularity which inevitably arises because the place where U-1 becomes singular is usually the most interesting point in the differential equation. Although it can be sidestepped by moving around in the complex plane, Stokes' phenomonon refers to the discrepancy in analytic continuations pass by one side or the other of such singularities.
In using the WKB decomposition (266) it is advantageous to begin with the largest term, treating the other as a perturbation. Normally the large term would be the diagonal matrix
![]() ,
solved as a system of one dimensional equations with the individual solutions
,
solved as a system of one dimensional equations with the individual solutions
| qi(t) | = | 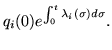 |
(267) |
Where P is rapidly changing, or changing slowly in a context of a nearly singular P, the second term should get priority. The classical turning point in quantum mechanical problems meets this specification, as would any other equation where P had the Jordan normal form and thus confluent eigenvalues.