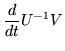 |
= | 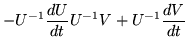 |
(268) |
| = | - U-1MV + U-1MV | (269) | |
| = | O. | (270) |
Consider the derivative of a quotient, U-1V, and suppose that U and V satisfy the same linear differential equation
dZ/dt = M Z:
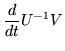 |
= | 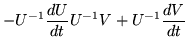 |
(268) |
| = | - U-1MV + U-1MV | (269) | |
| = | O. | (270) |
It should also be borne in mind that the equations could be solved starting from singular initial conditions, which would interfere with forming quotients. The conclusion that two solutions of the same equation are related by a factor supposes that neither is singular, in which case the proportionality constant C would be nonsingular too.
There is an interesting application of this result when the matrix of coefficients is periodic; that is, when
![]() for a constant period
for a constant period ![]() .
We have
.
We have
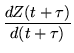 |
= | (271) | |
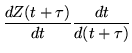 |
= | (272) | |
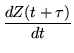 |
= | (273) |
Accordingly, Z(t) and ![]() ,
satisfying the same differential equation, are multiples,
,
satisfying the same differential equation, are multiples,
| (274) |
Mathematicians call this the Floquet theorem, whereas it is known to physicists as the Bloch theorem.
Symmetries other than translational are possible, for example reflection sending t into -t. The conclusions are similar: although the solutions do not need to have reflective symmetry, they can be built up from basic solutions which are themselves either even or odd.