| M | = | (275) | |
| Mo | = | (276) | |
| Ma | = | (277) |
The matrix of coefficients for a linear differential equation can be decomposed into the trace, a traceless symmetric tensor, and an antisymmetric tensor:
| M | = | (275) | |
| Mo | = | (276) | |
| Ma | = | (277) |
Solving for the antisymmetric part produces a rotation, because the differential equation for the inverse of the solution matrix has the same negative factor as the differential equation for the transpose. We have seen that two solutions of the same linear differential equation coincide whenever their initial values coincide.
When the system is two dimensional, there is only one antisymmetric matrix apart from scalar multiples, so that the solution is directly a matrix exponential, similar to what happens when the trace generates an exponential scale factor.
In any event, once the trace and antisymmetric part have been attended to, the final equation which remains has to deal with a rotating traceless symmetric tensor; this may or may not resemble an actual simplification.
One way to get a traceless coefficient matrix is to change the independent variable. In that case,
 |
= | 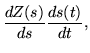 |
(278) |
| = | (279) | ||
| s(t) | = | 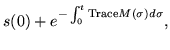 |
(280) |