Dependence of spectral density on mass

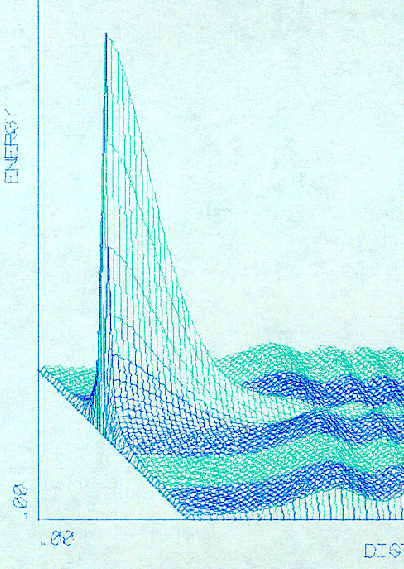
The weight function for the Stieltjes integral definition of the spectral density is substantially that it is the value at the origin of a wave function of unit amplitude at infinity. In order to better grasp this concept, Figure 10 repeats the resonance graph of Figure 5 (and those following it), having been truncated at the origin with a perspective showing the starting amplitude in clear outline.

  

Figure 10: The spectral density function is the absolute value at the origin of the wave function normalized to absolute value 1 at infinity. The reasonance has been sliced to show its behavior at the origin clearly.

Figure 11 exhibits another kind of graph which would be of interest, namely the result of showing only the trace across the origin featured in Figure 10, but for varying masses. The result could run from zero mass, without any classically forbidden region at all, to a large enough mass that it would correspond to actual electrons in atoms. That would be the limit which interested Sewell [5] and Titchmarsh [6].

  

Figure 11: The spectral density function is the absolute value at the origin of the wave function normalized to absolute value 1 at infinity. The apparent discontinuity in the second peak of the top figure is due to the egg-crate effect, and is not a break.

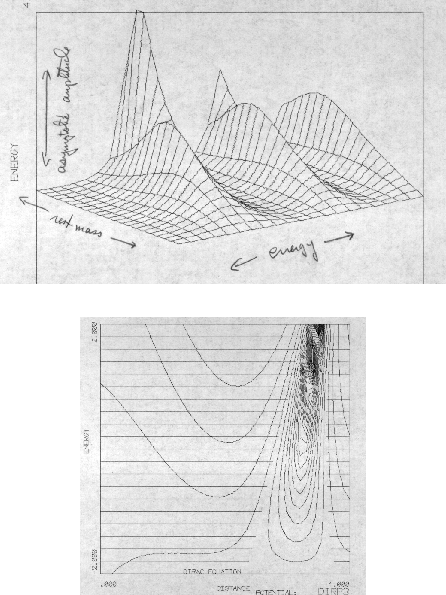The peaks in these functions, especially in the limit of large masses, suggest the interpretation of the Dirac harmonic oscillator in terms of complex energies and associated eigenfunctions.