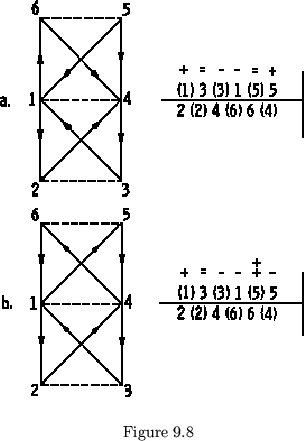In places where a right pat was slit instead of a left pat, it is
impossible to add more (for a new cycle) sides without suppressing others,
for the hinge joining two pats resulting from a
![]() flex joins the topmost
leaves in each pat and since the added leaf must be at the bottom of the
pat there would have to be a
flex joins the topmost
leaves in each pat and since the added leaf must be at the bottom of the
pat there would have to be a ![]() hinge connecting the top and bottom leaves
of the pat. This arrangement would suppress all in between sides. All of
the places in the cycle of an improper flexagon at which there are no degree
1 pats represent shortcuts, made by leaving at least two leaves in the left
pat. Thus, none of the diagonals of the map, which are shortcuts or just
plain ``cuts'' 9.1
can be added to in the conventional manner. That is, after
hinge connecting the top and bottom leaves
of the pat. This arrangement would suppress all in between sides. All of
the places in the cycle of an improper flexagon at which there are no degree
1 pats represent shortcuts, made by leaving at least two leaves in the left
pat. Thus, none of the diagonals of the map, which are shortcuts or just
plain ``cuts'' 9.1
can be added to in the conventional manner. That is, after
![]() flexing along an out-side edge or
flexing along an out-side edge or ![]() cut there will be a single leaf in
either the left or right pat. This leaf may be slit and a new side
revealed. There is a choice in slitting for all the slits after the
first until
cut there will be a single leaf in
either the left or right pat. This leaf may be slit and a new side
revealed. There is a choice in slitting for all the slits after the
first until ![]() slits have been made.
Thus, to any improper cycle it is possible
to add at a
slits have been made.
Thus, to any improper cycle it is possible
to add at a ![]() flex
flex ![]() cut another
cycle of any nature, so long as it too
has a
cut another
cycle of any nature, so long as it too
has a ![]() flex
flex ![]() cut in common with the
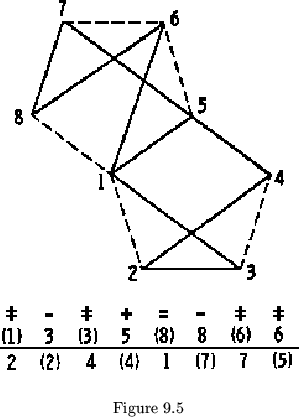
first cycle (see figure 9.5).
cut in common with the
first cycle (see figure 9.5).
Because of the nature of a shortcut, any ![]() cut tubulation also has a
single leaf in either the left or right pat. We have seen that we can
force the tubulation, rotate, and open up to the next side along the outside
edge or
cut tubulation also has a
single leaf in either the left or right pat. We have seen that we can
force the tubulation, rotate, and open up to the next side along the outside
edge or ![]() cut cycle 9.2.
What if we decide not to rotate but to slit the
single leaf instead? This opens up a new side which can only be reached
through the tubulation. Take, for example the single cycle improper
pentaflexagon shown in figure 9.6a. If we flex from 6 to 5, we may
tubulate to 3 by removing all but one leaf from the right hand pat (after
rotation). We can now force this tubulation, then, instead of rotating and
opening up to side 2, by a
cut cycle 9.2.
What if we decide not to rotate but to slit the
single leaf instead? This opens up a new side which can only be reached
through the tubulation. Take, for example the single cycle improper
pentaflexagon shown in figure 9.6a. If we flex from 6 to 5, we may
tubulate to 3 by removing all but one leaf from the right hand pat (after
rotation). We can now force this tubulation, then, instead of rotating and
opening up to side 2, by a ![]() flex or side 6 with a +1 flex, we may slit
the single right leaf and open up to a new side, 4 (see figure 9.6b).
From 4, it happens that we can rotate and
flex or side 6 with a +1 flex, we may slit
the single right leaf and open up to a new side, 4 (see figure 9.6b).
From 4, it happens that we can rotate and ![]() flex to 5. From 5, tubulate
to 3, and if we again force the tubulation and rotate, we can continue to
the three-cycle
flex to 5. From 5, tubulate
to 3, and if we again force the tubulation and rotate, we can continue to
the three-cycle ![]() .
If instead of rotating after forcing the tubulation, the same
flexing axis is maintained, we can flex to side 6.
.
If instead of rotating after forcing the tubulation, the same
flexing axis is maintained, we can flex to side 6.

There is, however, a much easier way to turn up the new side.
If we flex from 2 to 3, we can tubulate to 5, but if we force this tubulation
we cannot open up to 4 with a ![]() flex (although this may be accomplished
with a backwards flex). We can, however, open up to 4 without
forcing the tubulation but instead after tubulating, rotate the tubulation,
(by exchan-ging right for left pats) and open up with a forwards
flex to 4. Similarly, after we flex from 4 to 5, we may tubulate to 3,
but without forcing, we can rotate the tubulation and open up to side 1.
This method is much easier than the method involving forcing the tubulation.
The operation just described is called ``tubulating through''.
In constructing this type of flexagon
in the first place, it is much easier to tubulate
say from 3 to 5, rotate the tubulation, and then slit the single leaf in
the right hand pat to open up to 4.
flex (although this may be accomplished
with a backwards flex). We can, however, open up to 4 without
forcing the tubulation but instead after tubulating, rotate the tubulation,
(by exchan-ging right for left pats) and open up with a forwards
flex to 4. Similarly, after we flex from 4 to 5, we may tubulate to 3,
but without forcing, we can rotate the tubulation and open up to side 1.
This method is much easier than the method involving forcing the tubulation.
The operation just described is called ``tubulating through''.
In constructing this type of flexagon
in the first place, it is much easier to tubulate
say from 3 to 5, rotate the tubulation, and then slit the single leaf in
the right hand pat to open up to 4.
Returning to figure 9.6a, if we flex to 5 from 6, we could tubulate
to 3. If instead of forcing the tubulation, we were to rotate it and
slit the single left leaf, we would open up to a side, 4, which would
![]() flex instead of
flex instead of ![]() flex to 3 (see figure 9.6c). After rotation, we may
open up this tubulation by slitting one of two leaves depending whether
we wish a
flex to 3 (see figure 9.6c). After rotation, we may
open up this tubulation by slitting one of two leaves depending whether
we wish a ![]() cut flex or a shortcut flex. Then, from this side, we may
cut flex or a shortcut flex. Then, from this side, we may
![]() flex to 3 (see figure 9.6 d & e). Now let us reconsider the flexagon
shown in figure 9.6b. If we flex from side 4 to side 5, we find that
after rotation there is a single leaf in the left hand pat. Also, this
single leaf is connected to the lowest leaf in the right pat, which means
that either leaf may be slit without suppressing another side (call this
choice ``A''). Whichever one we slit, we may flex to a new side which then
tubulates to side 3. This tubulation may be opened in three ways, (choice
``B'') in the manner we have used for all tubulations. Whichever way we do
it, we can flex back to side 3.
flex to 3 (see figure 9.6 d & e). Now let us reconsider the flexagon
shown in figure 9.6b. If we flex from side 4 to side 5, we find that
after rotation there is a single leaf in the left hand pat. Also, this
single leaf is connected to the lowest leaf in the right pat, which means
that either leaf may be slit without suppressing another side (call this
choice ``A''). Whichever one we slit, we may flex to a new side which then
tubulates to side 3. This tubulation may be opened in three ways, (choice
``B'') in the manner we have used for all tubulations. Whichever way we do
it, we can flex back to side 3.
This completes a separate improper cycle joined to the original by a tubulation. Choice ``B'' decides which of three improper cycles will be added, and choice ``A'' determines how it will be oriented with respect to the original cycle. If we agree to slit the left most leaf in choice ``B'', slitting the left leaf in choice ``A'' will give the map in figure 9.7a, while slitting the lowest right leaf will produce the map in Figure 9.7b.
This method of adding more cycles attached by tubulations may be
extended to include the ![]() flexagon. We may tubulate through from any
tubulation which is on the
flexagon. We may tubulate through from any
tubulation which is on the ![]() cut cycle by tubulating, rotating, and slitting
the single leaf. After we have completed a series of
cut cycle by tubulating, rotating, and slitting
the single leaf. After we have completed a series of ![]() flexes (and if
nece-ssary, slittings) which leads back to the side across the tubulation,
we have a choice of two possible leaves to slit to start the series of
flexes which will complete the cycle. The orientation of the new cycle will
be determined by this slitting
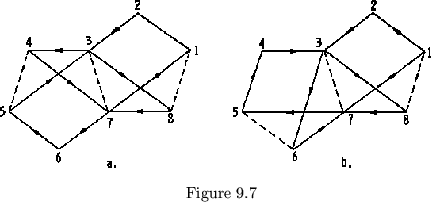
(in symmetrical cycles, such as in
tetraflexagons, this di-fference in
orientation will appear to be a
reversal of vectors - see figure
9.8). When all cycles are completed,
the flexagon must be renumbered by
folding the unit together and numbering the leaves consecutively down the
unit
flexes (and if
nece-ssary, slittings) which leads back to the side across the tubulation,
we have a choice of two possible leaves to slit to start the series of
flexes which will complete the cycle. The orientation of the new cycle will
be determined by this slitting
(in symmetrical cycles, such as in
tetraflexagons, this di-fference in
orientation will appear to be a
reversal of vectors - see figure
9.8). When all cycles are completed,
the flexagon must be renumbered by
folding the unit together and numbering the leaves consecutively down the
unit
![]() .
.