Another justification for the use of negative face degrees is the
use of ne-gative leaf angles. We have already built triflexagons from
leaves having negative angles, in section V. Negative angles were the
result of continuously deforming the leaves from ordinary positive
angles, through ![]() angles, to negative angles. To again distinguish
such flexagons from ordinary ones, we assume that the face degree, which
equals
angles, to negative angles. To again distinguish
such flexagons from ordinary ones, we assume that the face degree, which
equals
![]() , where
, where
![]() is the angle between the hinges of
the leaf, is continuous for all values of
is the angle between the hinges of
the leaf, is continuous for all values of ![]() . This gives the accepted
positive and negative values for the face degree.
. This gives the accepted
positive and negative values for the face degree.
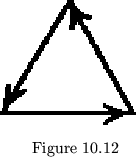
In section V, we treated flexagons of cycle 3, such as that
shown in figure 10.12, for various possible face degrees. Since the
sum of the face degrees, taken with the arrows all pointing in the same
direction, must be zero, we let two of the faces be of degree ![]() , making
the other of degree
, making
the other of degree ![]() . Thus, for
. Thus, for
![]() , as when equilateral
triangles are used,
, as when equilateral
triangles are used,
![]() , and all the faces are alike. For
higher classes,
, and all the faces are alike. For
higher classes,
![]() ;
;
![]() ; and
; and
![]() is either
is either
![]() or negative.
or negative.
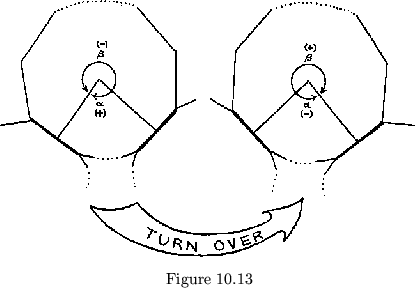
It is interesting that, in deforming the leaves to give them negative angles, not only is the upper side placed underneath the flexagon, but its center moves to its outer edge. We defined the face degree as the angle between the perpendiculars on the hinges entering and leaving each pat. This definition allows enough ambiguity to explain the presence of two face degrees at each position, for we did not specify the direction of measurement of the angle. Consistent with the observation that in a negative face the ``central angles'' of the flexagon point away from the center, is the fact that if the angle between the perpendiculars is measured not so that it includes the center, but across the outer edge of the flexagon, where the negative leaf angles ``point'' (See fig. 10.13), it turns out to be negative. Also, when a flexagon is turned over, the signs of the two angles are automatically reversed (see fig. 10.13). When the sign of a face degree is not specifically given, it is to be assumed that we are referring to the face with a positive face degree.
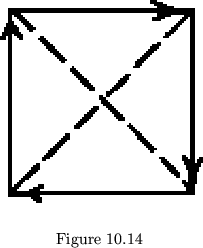
When we come to making negative-angled flexagons of cycles other
than 3, we find ourselves putting hinges across places that were considered
in section V to lie ``at infinity'', or were not (for some reason
or other) allowed to have hinges. Thus, the flexagon in fig. 10.14 has
hinges at ``infinity'' during both tubulations. Fortunately, the dubious
concepts of ``angles at infinity'', and so forth, are not critical to the
theory, and everything said so far applies equally well to flexagons
of all cycles. The only difference is that an increase in cycle prohibits
a decrease below ![]() of hinge positions. Since we have mentioned
the tubulation in tetraflexagons, it is worth pointing out that its face
degree,
of hinge positions. Since we have mentioned
the tubulation in tetraflexagons, it is worth pointing out that its face
degree,
![]() , makes it meaningless to place an arrow along it,
since all of its faces have equal face degrees.
, makes it meaningless to place an arrow along it,
since all of its faces have equal face degrees.
In conclusion, it might be said that when one actually comes upon a face with a negative face degree, probably the simplest, least confusing procedure is to turn it over and forget all about the whole thing.