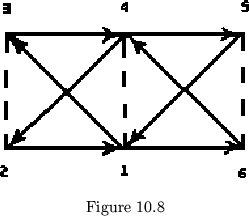
Yet another problem of face degrees and leaf angles lies before us. To introduce this problem, we return to the ``tubulation'' of tetraflexagons. Let us study this type of face more carefully. The improper flexagon shown in fig. 10.8 will suffice for demonstration purposes. Suppose we leave face (1,6) and open up so that sides 1 and 4 show 10.2.

Side 4 will be on the inside, side 1 on the outside. We find that we can change faces a number of ways; folding the tube flat the way it was opened out gives back (1,6) if we reopen from the bottom, (1,5) if we reopen from the top. Folding the tube flat the other possible way gives the two corresponding faces (1,3) and (1,2). If we turn the tube over, so that the other end is upward, we get the faces (6,1), (5,1), (3,1) and (2,1). These are all the faces possible.
In order to deal effectively with such flexagons as this, we
must correlate the operations just described with those already employed
with ![]() faces. In order to obtain a system as simple and universal as
possible, we maintain our former policy of minimizing class
differences. Thus, since flexing has heretofore replaced one side
(the lower side) by a new side, while moving the other (upper) side,
we define this as flexing, for all kinds of faces. This, then,
establishes which side of the flexagon is up; the sides of each face
can now always be ordered. Turning over will be the operation that
changes the order of the sides in the face. This ordering of the
sides is, of course, distinct from the ordering of the pats. Just
as turning over reverses the order of the sides, so we define rotation
as reversal of the pat order. As we would naturally expect, rotation
of the
faces. In order to obtain a system as simple and universal as
possible, we maintain our former policy of minimizing class
differences. Thus, since flexing has heretofore replaced one side
(the lower side) by a new side, while moving the other (upper) side,
we define this as flexing, for all kinds of faces. This, then,
establishes which side of the flexagon is up; the sides of each face
can now always be ordered. Turning over will be the operation that
changes the order of the sides in the face. This ordering of the
sides is, of course, distinct from the ordering of the pats. Just
as turning over reverses the order of the sides, so we define rotation
as reversal of the pat order. As we would naturally expect, rotation
of the ![]() face meant squashing it flat another way. As for turning
over, it was done in the
face meant squashing it flat another way. As for turning
over, it was done in the ![]() face by rotating it
face by rotating it
![]() end over end.
Again as expected, this merely reversed the order of all the succeeding pats.
However, flexing does not receive so simple a diagnosis as
this operation.
end over end.
Again as expected, this merely reversed the order of all the succeeding pats.
However, flexing does not receive so simple a diagnosis as
this operation.
Since we flexed from face (1,6) to a new face with sides 4 and 6,
side 6 must, in the tubulation, be the side defined as the ``lower'' side.
This makes sense if we think of the tubulation as a limiting case of
face degrees less than
![]() , as in Section V. To flex again, we will
be required to fold together the surfaces marked 6. However, we cannot
do this without moving 6 to the inside of the tube. Previously, we
have been able to ``push through'' the flexagon, this operation being
that which moves the flexagon from the position in which the upper
side can be folded together to that in which the lower side can be folded
together. This operation is inherently dependent upon the class and face
degrees of the particular flexagon, therefore having no relationship to the
other operations, except in that it is necessary to ``push through'' a
flexagon to flex it. Thus, if a flexagon cannot be ``pushed through'' at a
given face, it will not be able to leave that face except through using
the side by which it arrived at it. The effect of this on the map is
as if the face line were broken. A face can be pushed through only if
the sum of the angles between the hinges, about the center of the flexagon,
is at least
, as in Section V. To flex again, we will
be required to fold together the surfaces marked 6. However, we cannot
do this without moving 6 to the inside of the tube. Previously, we
have been able to ``push through'' the flexagon, this operation being
that which moves the flexagon from the position in which the upper
side can be folded together to that in which the lower side can be folded
together. This operation is inherently dependent upon the class and face
degrees of the particular flexagon, therefore having no relationship to the
other operations, except in that it is necessary to ``push through'' a
flexagon to flex it. Thus, if a flexagon cannot be ``pushed through'' at a
given face, it will not be able to leave that face except through using
the side by which it arrived at it. The effect of this on the map is
as if the face line were broken. A face can be pushed through only if
the sum of the angles between the hinges, about the center of the flexagon,
is at least
![]() . Thus we can break map lines by building
flexagons some or all of whose faces do not satisfy this requirement.
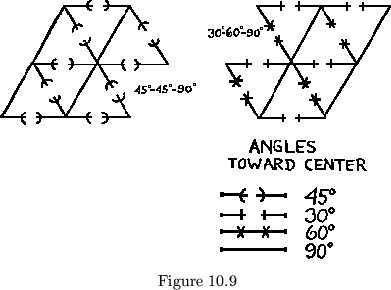
In cup flexagons, for example, every map path is broken. Other interesting
flexagons of this type may be made from
. Thus we can break map lines by building
flexagons some or all of whose faces do not satisfy this requirement.
In cup flexagons, for example, every map path is broken. Other interesting
flexagons of this type may be made from
![]() or
or
![]() triangles, with
two units (See fig. 10.9). In faces of degree
triangles, with
two units (See fig. 10.9). In faces of degree
![]() , such
as the tubulation, the hinges are parallel, and no number of units will
suffice to allow pushing through. Hence in this case the map path is
always broken. If we should extend the ``pushing through'' operation to
include the non-trivial case of actually cutting open the tubulation and
winding it up the other way, flexing would occur unimpeded. Thus we
choose to say that ``pushing through'' is impeded, rather than flexing
itself. This lets flexing remain independent of the sum of the angles
about the flexagon's center.
, such
as the tubulation, the hinges are parallel, and no number of units will
suffice to allow pushing through. Hence in this case the map path is
always broken. If we should extend the ``pushing through'' operation to
include the non-trivial case of actually cutting open the tubulation and
winding it up the other way, flexing would occur unimpeded. Thus we
choose to say that ``pushing through'' is impeded, rather than flexing
itself. This lets flexing remain independent of the sum of the angles
about the flexagon's center.
Well, if we cannot flex away from face (4,1) without turning over or cutting the flexagon, how exactly did we attain the faces that we did? In terms of the operations already known, the transition from (4,1 ) to (1,6) was clearly equivalent to turning over, flexing and turning over again. Not counting the rotation this was the same operation that brought us to (1,3). It is called a back-flex, since it is the reverse of flexing. A back-flex differs from a flex only in the side (lower or upper) that is folded together, since turning the flexagon over makes the back-flex a flex and the flex a back-flex. The operation bringing us to faces (1,5) and (1,2) must have been a back-flex, since it folded together side 4.
It may have been noticed that something is strange about faces (1,5) and (1,2). Although side 1 is technically the ``upper'' side (the side to be folded together by the next back-flex), it appears on the underside of the flexagon. Thus a subsequent back-flex will look exactly like a normal flex. Such a face, in which the ``lower'' side is on top, is described by affixing a negative sign to its face degree. Doing this is justifiable in several ways.
First, it has been seen that the hinge position used in flexing
determines the face degree of the next face. The hinge position, like
the face degree, can be measured in degrees, and is, in fact, the same
as the face degree of the next face. Since any face in which the new
side is to appear on the bottom of the flexagon opens out from the bottom,
and therefore has its new hinge toward the top of the folded-together
flexagon, the new hinge will be in a position between
![]() and
and
![]() . For face degrees, however, we will use only those angles
between
. For face degrees, however, we will use only those angles
between
![]() and
and
![]() , so that the upside-down faces have negative
face degrees. We can see that it is not sufficient to give only the
face degree of a given face, since there are now four face degrees per
face. For a face comprising the two sides
, so that the upside-down faces have negative
face degrees. We can see that it is not sufficient to give only the
face degree of a given face, since there are now four face degrees per
face. For a face comprising the two sides ![]() and
and ![]() , either side may be
on top, and either side may be the ``upper'' side. Thus the form faces are
, either side may be
on top, and either side may be the ``upper'' side. Thus the form faces are
![]() . 10.3
. 10.3
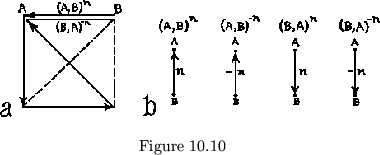
There, will be four faces, related like these, whenever there is at
least one. Given one of these faces, we will be able to reach other
faces, made up of other sides, using flexes and rotations. Using these
operations only, we can reach two and only two faces in each set of four,
by following routes similar to that shown in fig. 10.10a. As we see from
the figure the two related faces look exactly alike, but different sides
are folded together in flexing. Doing this is equivalent to changing
the flexing direction without turning the flexagon over. Thus the total
number of faces breaks down into two equal families, the member of
one of which can only be reached from members of the other by means
of turning over. To distinguish among the various faces in the map,
we mark each path with a face degree, and also indicate the ``upper''
side, by drawing an arrow from the ``lower'' to the ``upper'' side. Thus
the faces made up of the two sides, ![]() and
and ![]() , are represented as in
Figure 10.10b. Turning the flexagon over, which changes face
, are represented as in
Figure 10.10b. Turning the flexagon over, which changes face ![]() into face
into face ![]() , is seen to reverse the direction of the arrow. The
two faces that can be reached from one another by changing the flexing
direction as in figure 10.10a, and which look alike, have both arrows
and signs reversed. In actually using the map, we choose one in each
set of four faces and mark it upon the map. The others must be figured
out as needed. It helps to remember (1) that flexing backwards means
that the flexing direction has been reversed, so that one travels against
all the arrows and the signs of all the faces are wrong, and (2) that
turning the flexagon over makes all the arrows point the wrong way or
(if the flexing direction is reversed also) makes all the face degrees
have the wrong sign. Thus, since in reaching faces (1,5) and (1,2) we
traveled against a
, is seen to reverse the direction of the arrow. The
two faces that can be reached from one another by changing the flexing
direction as in figure 10.10a, and which look alike, have both arrows
and signs reversed. In actually using the map, we choose one in each
set of four faces and mark it upon the map. The others must be figured
out as needed. It helps to remember (1) that flexing backwards means
that the flexing direction has been reversed, so that one travels against
all the arrows and the signs of all the faces are wrong, and (2) that
turning the flexagon over makes all the arrows point the wrong way or
(if the flexing direction is reversed also) makes all the face degrees
have the wrong sign. Thus, since in reaching faces (1,5) and (1,2) we
traveled against a ![]() face arrow, the result is a
face arrow, the result is a ![]() face with 1
rather than 5 as the upper side, although 5 is on top; the map shown
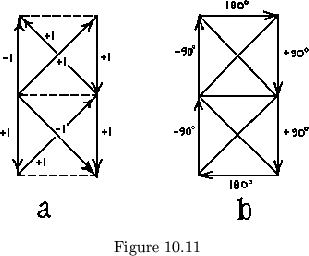
in figure 10.8 could also be drawn as in figure 10.11a.
face with 1
rather than 5 as the upper side, although 5 is on top; the map shown
in figure 10.8 could also be drawn as in figure 10.11a.
This raises another question, which results in fairly fruitful
study. Just which of the four possible faces in each set are we to
mark upon the map? In all cases, we will label a given map with the
members of either one of the two families of faces (but not both), thus
establishing a distinction between the flexagon in a given position and
the same flexagon turned over. Which family we choose is irrelevant.
Between the two possible faces remaining at each position, there is no
such distinction, so that they may be mixed in any way. So far, we have
consistently chosen the face in each pair with the positive face degree.
There is, however, another method worth considering. This method deals
only with the paths on the outer edge of the map; other faces may be
marked with either possible face. Considering only the outer faces, then,
we find that they form a simple closed curve, enclosing the rest of the
map. The arrows are placed on this curve so that they always point the
same direction, clockwise or counterclockwise about the map. They are
then labeled with the appropriate signs (See fig. 10.11b). The interesting
thing about this method of labeling is that it gives the sign sequence
signs corresponding to each outer face. These are equal to the
face degrees shown. We can now, for the first time, make use of the
generality with which flexing has been treated, in proving this fact.
Flexing along an ![]() cut cycle without rotations shows the sub-pats
corresponding to each face, with each one alone making up a pat at its face.
Also, since the single-sub-pat pat alternates between the two pats, as
well as inverting itself, during each flex, the sign or sum of the signs
of the leaves in each single-sub-pat pat is always equal to the face
degree (or the negative of the face degree; this point is irrelevant).
In alternate cycles, we will travel the opposite way about the cycle.
However, in changing cycles, we rotate after flexing so that the single-subpat
pat occurs in the same position as it last did. This makes the
face degree equal to the negative of the sum of the signs of the leaves
in the single-subpat pat, rather than equal to it. Thus, if we draw
the vectors the wrong way about alternate cycles, as we do when we draw
them head-to-tail all about the edge of the map, the face degree will
always equal the sum of the signs in the single subpat. These are the
signs themselves, in the edge of the map. Q.E.D.
cut cycle without rotations shows the sub-pats
corresponding to each face, with each one alone making up a pat at its face.
Also, since the single-sub-pat pat alternates between the two pats, as
well as inverting itself, during each flex, the sign or sum of the signs
of the leaves in each single-sub-pat pat is always equal to the face
degree (or the negative of the face degree; this point is irrelevant).
In alternate cycles, we will travel the opposite way about the cycle.
However, in changing cycles, we rotate after flexing so that the single-subpat
pat occurs in the same position as it last did. This makes the
face degree equal to the negative of the sum of the signs of the leaves
in the single-subpat pat, rather than equal to it. Thus, if we draw
the vectors the wrong way about alternate cycles, as we do when we draw
them head-to-tail all about the edge of the map, the face degree will
always equal the sum of the signs in the single subpat. These are the
signs themselves, in the edge of the map. Q.E.D.
Since this is true, we can now easily find sign sequences for any flexagon, and, moreover, by drawing vectors all in the same direction about the edge of a map whose face degrees are unknown, and then labeling the faces with corresponding signs from a given sign sequence, we can determine the type of faces present in an unexplored map.